ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 2 Fractions and Decimals Ex 2.3
Question 1.
Evaluate the following:

Solution:

Question 2.
Find:

Solution:


Question 3.
Evaluate the following:

Solution:

Question 4.
Find the value of:

Solution:


Question 5.
Which is greater:
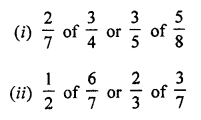
Solution:


Question 6.
If 1 metre cloth costs ₹ 31\(\frac { 3 }{ 4 }\), find the cost of 5\(\frac { 1 }{ 2 }\) metres cloth.
Solution:

Question 7.
If the speed of a car is 105\(\frac { 1 }{ 5 }\) km/h, find the distance covered by it in 3\(\frac { 3 }{ 5 }\) hours.
Solution:
Speed of a car = 105\(\frac { 1 }{ 5 }\) km/h = \(\frac { 526 }{ 5 }\) km/h
It will covered a distance in 3\(\frac { 3 }{ 5 }\) hours

Question 8.
A car runs 16 km using 1 litre of petrol. How much distance will it cover in 2\(\frac { 3 }{ 4 }\) litres of petrol?
Solution:
A car runs in 1 litre of petrol = 16 km
It will run in 2\(\frac { 3 }{ 4 }\) litres of petrol

Question 9.
Sushant reads \(\frac { 1 }{ 3 }\) part of a book in 1 hour. How much part of the book will he read in 2\(\frac { 1 }{ 5 }\) hours?
Solution:
Sushant reads a book in 1 hour = \(\frac { 1 }{ 3 }\) part
He will read it in 2\(\frac { 1 }{ 5 }\) hours

Question 10.
An ornament is made of gold and copper and weighs 52 grams. If \(\frac { 2 }{ 13 }\) of its part is copper, find the weight of pure gold in it.
Solution:
Weight of ornament = 52 grams
In it \(\frac { 2 }{ 13 }\) part is copper
Weight of copper = 52 × \(\frac { 2 }{ 13 }\) = 8 grams
Then weight of gold = 52 grams – 8 grams = 44 grams
Question 11.
In a class of 40 students, \(\frac { 1 }{ 5 }\) of the total number of students like to study English and \(\frac { 2 }{ 5 }\) of the total number of students like to study Mathematics and the remaining like to study Science.
(i) How many students like to study English?
(ii) How many students like to study Mathematics?
(iii) What fraction of the total number of students like to study Science?
Solution:
The number of students in a class = 40
(i) Number of students who like English = \(\frac { 1 }{ 5 }\) of 40 = 8 students
(ii) Number of students who like Mathematics = \(\frac { 2 }{ 5 }\) of 40 = 16 students
(iii) Remaining students = 40 – (8 + 16) = 40 – 24 = 16 students
Number of students who like Science = 16
Fraction of students = \(\frac { 16 }{ 40 }\) = \(\frac { 2 }{ 5 }\)
Question 12.
A rectangular sheet of paper is 12\(\frac { 1 }{ 2 }\) cm long and 10\(\frac { 2 }{ 3 }\) cm wide. Find its
(i) perimeter
(ii) area
Solution:
Length of rectangular sheet of paper = 12\(\frac { 1 }{ 2 }\) cm = \(\frac { 25 }{ 2 }\) cm
and breadth = 10\(\frac { 2 }{ 3 }\) = \(\frac { 32 }{ 3 }\) cm

Question 13.
In a school, \(\frac { 25 }{ 54 }\) of the students are girls and the rest are boys. If the number of boys is 2030, find the number of girls.
Solution:
In a school,
Number of girls = \(\frac { 25 }{ 54 }\)
Then, number of boys = 1 – \(\frac { 25 }{ 54 }\) = \(\frac { 29 }{ 54 }\)
Number of boys = 2030
\(\frac { 29 }{ 54 }\) of total students = 2030
Total number of students = 2030 × \(\frac { 54 }{ 29 }\) = 3780
Number of girls = 3780 – 2030 = 1750
Question 14.
In an orchard, \(\frac { 1 }{ 5 }\) are orange grees, \(\frac { 3 }{ 13 }\) are mango trees and the rest are banana trees. If the banana trees are 148 in number, find the total number of trees in the orchard.
Solution:
In an orchard,
Orange trees = \(\frac { 1 }{ 5 }\) part
Mango trees = \(\frac { 3 }{ 13 }\) part
Banana trees = Rest
