Selina Concise Mathematics class 7 ICSE Solutions – Fundamental Concepts (Including Fundamental Operations)

Selina Concise Mathematics class 7 ICSE Solutions – Fundamental Concepts (Including Fundamental Operations)

ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions

APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 7 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 7 with Free PDF download option. Selina Publishers Concise Mathematics for Class 7 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.

Selina Class 7 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics

POINTS TO REMEMBER

1. Constants and Variables : The numbers which has fixed value is called constant and same at English alphabet which can be assigned any value according to the requirement is called variables.
2. Term : A term is a number, (constant), a variable or a combination of numbers and variables.
3. Algebraic Expression : An algebraic expression is a collection of one or more terms, which are separated from each other by addition (+) or subtraction (-) signs.
4. Types of algebraic expressions :
   (i) Monomial : It has only one term
   (ii) Binomial : It has two terms
   (iii) Trinomial : It has three terms
   (iv) Multinomial : It has more than three terms
   (v) Polynomial : It has two or more than two terms.
   Note : An expression of the type \(\frac { 2 }{ 5 }\) does not form a monomial unless JC is not equal to zero.
5. Product: When two or more quantities are multiplied together, the result is called their product.
6. Factors : Each of the quantities (numbers or variables) multiplied together to form a term is called a factor of the given term.
7. Co-efficient: In a monomial, any factor or group of factors of a term is called the co-efficient of the remaining part of the monomial.
8. Degree of a monomial: The degree of a monomial is the exponent of its variable or the sum of the exponents of its variables.
9. Degree of a polynomial: The degree of a polynomial is the degree of its highest degree term.
10. Like and unlike terms : Terms having the same literal co-efficients or alphabetic letters are called like terms ; whereas the terms with different literal co-efficients are called unlike terms.
11. Addition and subtraction : Addition and subtraction of only like terms is possible by adding or subtracting the numerical co-efficients.
12. Multiplication and division :
    (A) Multiplication :
    (i) Multiplications of monomials.
    (a) Multiply the numerical co-efficient together
    (ii) Multiply the literal co-efficients separately together.
    (iii) Combine the like terms.
    (B) Division :
    (i) Dividing a polynomial by a monomial Divide each term of the polynomial by monomial and simplify each fractions.
    (ii) While dividing one polynomial by another polynomial ; arrange the terms of both the dividend and the divisior both in descending or in ascending order of their powers and then divide.

SOME IMPORTANT POINTS

TYPES OF BRACKETS:
The name of different types of brackets and the order in which they are removed is shown below:
(a) ____ ; Bar (Vinculum) bracket
(b) ( ); Circular bracket .
(c) { } ; Curly bracket and then
(d) [ ]; square bracket

EXERCISE 11 (A)

Question 1.
Separate constant terms and variable terms from tile following :

Solution:

Constant is only 8 others are variables

Question 2.
Constant is only 8 others are variables
(i) 2x ÷ 15
(ii) ax+ 9
(iii) 3x² × 5x
(iv) 5 + 2a-3b
(v) 2y – \(\frac { 7 }{ 3 }\) z÷x
(vi) 3p x q ÷ z
(vii) 12z ÷ 5x + 4
(viii) 12 – 5z – 4
(ix) a³ – 3ab² x c

Answer:

Question 3.
Write the coefficient of:
(i) xy in – 3axy
(ii) z² in p²yz²
(iii) mn in -mn
(iv) 15 in – 15p²

Solution:
(i) Co-efficient of xy in – 3 axy = – 3a
(ii) Co-efficient of z² in p²yz² = p²y
(iii) Co-efficient of mn in – mn = – 1
(iv) Co-efficient of 15 in – 15p² is -p²

Question 4.
For each of the following monomials, write its degree :
(i) 7y
(ii) – x²y
(iii) xy²z
(iv) – 9y²z³
(v) 3 m³n⁴
(vi) – 2p²q³r⁴

Solution:
(i) Degree of 7y = 1
(ii) Degree of – x²y = 2+1=3
(iii) Degree of xy²z = 1 + 2 + 1 = 4
(iv) Degree of – 9y²z³ = 2 + 3 = 5
(v) Degree of 3m³n⁴ = 3 + 4 = 7
(vi) Degree of – 2p²q³r⁴ = 2 + 3 + 4 = 9

Question 5.
Write the degree of each of the following polynomials :
(i) 3y³-x²y² + 4x
(ii) p³q² – 6p²q⁵ + p⁴q⁴
(iii) – 8mn⁶+ 5m³n
(iv) 7 – 3x²y + y²
(v) 3x – 15
(vi) 2y²z + 9yz³

Solution:
(i) The degree of 3y³ – x²y²+ 4x is 4 as x²
y² is the term which has highest degree.
(ii) The degree of p³q² – 6p²q⁵-p⁴q⁴ is 8 as p⁴ q⁴ is the term which has highest degree.
(iii) The degree of- 8mn⁶ + 5m³n is 7 as – 8mx⁶ is the term which has the highest degree.
(iv) The degree of 7 – 3x² y + y² is 3 as – 3x²y is the term which has the highest degree.
(v) The degree of 3x – 15 is 1 as 3x is the term which is highest degree.
(vi) The degree of 2y² z + 9y z³ is 4 as 9yz³ has the highest degree.

Question 6.
Group the like term together :
(i) 9x², xy, – 3x², x² and – 2xy
(ii) ab, – a²b, – 3ab, 5a²b and – 8a²b
(iii) 7p, 8pq, – 5pq – 2p and 3p

Solution:
(i) 9x², – 3x² and x² are like terms
xy and – 2xy are like terms
(ii) ab, – 3ab, are like terms,
– a²b, 5a²b, – 8a²b are like terms
(iii) 7p, – 2p and 3p are like terms,
8pq, – 5pq are like terms.

Question 7.
Write numerical co-efficient of each of the followings :
(i) y
(ii) -y
(iii) 2x²y
(iv) – 8xy³
(v) 3py²
(vi) – 9a²b³

Solution:
(i) Co-efficient of y = 1
(ii) Co-efficient of-y = – 1
(iii) Co-efficient of 2x2y is = 2
(iv) Co-efficient of – 8xy3 is = – 8
(v) Co-efficient of Ipy2 is = 3
(vi) Co-efficient of – 9a2b3 is = – 9

Question 8.
In -5x³y²z⁴; write the coefficient of:
(i) z²
(ii) y²
(iii) yz²
(iv) x³y
(v) -xy²
(vi) -5xy²z
Also, write the degree of the given algebraic expression.

Solution:
-5x³y²z⁴
(i) Co-efficient of z2 is -5x³y²z²
(ii) Co-efficient of y2 is -5x³z⁴
(iii) Co-efficient of yz² is -5x³yz²
(iv) Co-efficient of x³y is -5yz⁴
(v) Co-efficient of -xy² is 5x²z⁴
(vi) Co-efficient of -5xy²z is x²z³
Degree of the given expression is 3 + 2 + 4 = 9

EXERCISE 11 (B)

Question 1.
Fill in the blanks :
(i) 8x + 5x = ………
(ii) 8x – 5x =……..
(iii) 6xy² + 9xy² =……..
(iv) 6xy² – 9xy² = ………
(v) The sum of 8a, 6a and 5b = ……..
(vi) The addition of 5, 7xy, 6 and 3xy = …………
(vii) 4a + 3b – 7a + 4b = ……….
(viii) – 15x + 13x + 8 = ………
(ix) 6x²y + 13xy² – 4x²y + 2xy² = ……..
(x) 16x² – 9x² = and 25xy² – 17xy²=………

Solution :

Question 2.
Add :
(i)- 9x, 3x and 4x
(ii) 23y², 8y² and – 12y²
(iii) 18pq – 15pq and 3pq

Solution:

Question 3.
Simplify :
(i) 3m + 12m – 5m
(ii) 7n² – 9n² + 3n²
(iii) 25zy—8zy—6zy
(iv) -5ax² + 7ax² – 12ax²
(v) – 16am + 4mx + 4am – 15mx + 5am

Solution:

Question 4.
Add : 
(i) a + i and 2a + 3b
(ii) 2x + y and 3x – 4y
(iii)- 3a + 2b and 3a + b
(iv) 4 + x, 5 – 2x and 6x

Solution:

Question 5.
Find the sum of:
(i) 3x + 8y + 7z, 6y + 4z- 2x and 3y – 4x + 6z
(ii) 3a + 5b + 2c, 2a + 3b-c and a + b + c.
(iii) 4x²+ 8xy – 2y² and 8xy – 5y² + x²
(iv) 9x² – 6x + 7, 5 – 4x and 6 – 3x²
(v) 5x² – 2xy + 3y² and – 2x² + 5xy + 9y²
and 3x² -xy- 4y²
(vi) a² + b² + 2ab, 2b² + c² + 2bc
and 4c²-a² + 2ac
(vii) 9ax – 6bx + 8, 4ax + 8bx – 7
and – 6ax – 46x – 3
(viii) abc + 2 ba + 3 ac, 4ca – 4ab + 2 bca
and 2ab – 3abc – 6ac
(ix) 4a² + 5b² – 6ab, 3ab, 6a² – 2b²
and 4b² – 5 ab
(x) x² + x – 2, 2x – 3x² + 5 and 2x² – 5x + 7
(xi) 4x³ + 2x² – x + 1, 2x³ – 5x²– 3x + 6, x² + 8 and 5x³ – 7x

Solution:

Question 6.
Find the sum of:
(i) x and 3y
(ii) -2a and +5
(iii) – 4x² and +7x
(iv) +4a and -7b
(v) x³+3x²y and 2y²
(vi) 11 and -by

Solution:

Question 7.
The sides of a triangle are 2x + 3y, x + 5y and 7x – 2y, find its perimeter.

Solution:

Question 8.
The two adjacent sides of a rectangle are 6a + 96 and 8a – 46. Find its, perimeter.

Solution

Question 9.
Subtract the second expression from the first:

Solution:

Question 10.
Subtract:

Solution:

Question 11.
Subtract – 5a² – 3a + 1 from the sum of 4a² + 3 – 8a and 9a – 7.

Solution:

Question 12.
By how much does 8x³ – 6x² + 9x – 10 exceed 4x³ + 2x² + 7x -3 ?

Solution:

Question 13.
What must be added to 2a³ + 5a – a² – 6 to get a² – a – a³ + 1 ?

Solution:

Question 14.
What must be subtracted from a² + b² + lab to get – 4ab + 2b² ?

Solution:

Question 15.
Find the excess of 4m² + 4n² + 4p² over m²+ 3n² – 5p²

Solution:

Question 16.
By how much is 3x³ – 2x²y + xy² -y³ less than 4x³ – 3x²y – 7xy² +2y³

Solution:

Question 17.
Subtract the sum of 3a² – 2a + 5 and a² – 5a – 7 from the sum of 5a² -9a + 3 and 2a – a² – 1

Solution:

Question 18.
The perimeter of a rectangle is 28x³+ 16x² + 8x + 4. One of its sides is 8x² + 4x. Find the other side

Solution:

Question 19.
The perimeter of a triangle is 14a² + 20a + 13. Two of its sides are 3a² + 5a + 1 and a² + 10a – 6. Find its third side.

Solution:

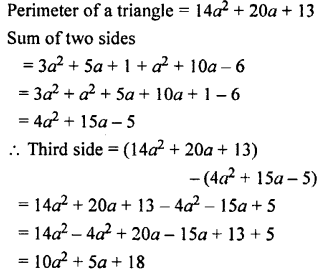
Question 20.

Solution:

Question 21.

Solution:

Question 22.
Simplify:

Solution:

EXERCISE 11 (C)

Question 1.
Multiply:

Solution:

Question 2.
Copy and complete the following multi-plications :

Solution:

Question 3.
Evaluate :

Solution:

Question 4.
Evaluate:

Solution:

Question 5.
Evaluate :

Solution:

Question 6.
Multiply:

Solution:

Question 7.
Multiply:

Solution:

EXERCISE 11 (D)

Question 1.
Divide:

Solution:

Question 2.
Divide :

Solution:

Question 3.
The area of a rectangle is 6x²– 4xy – 10y² square unit and its length is 2x + 2y unit. Find its breadth

Solution:

Question 4.
The area of a rectangular field is 25x² + 20xy + 3y² square unit. If its length is 5x + 3y unit, find its breadth, Hence find its perimeter.

Solution:

Question 5.
Divide:

Solution:

EXERCISE 11 (E)

Simplify
Question 1.

Solution:

Question 2.

Solution:

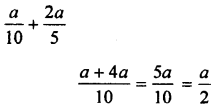
Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

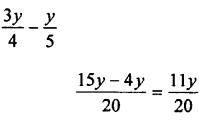
Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.

Solution:

Question 19.

Solution:

Question 20.

Solution:

Question 21.

Solution:

Question 22.

Solution:

Question 23.

Solution:

Question 24.

Solution:

Question 25.

Solution:

Question 26.

Solution:

EXERCISE 11 (F)

Enclose the given terms in brackets as required :

Question 1.
 x – y – z = x-{…….)

Solution:
x – y – z = x – (y + z)

Question 2.
x² – xy² – 2xy – y² = x² – (…….. )

Solution:
x² – xy² – 2xy – y²
= x² – (xy² + 2xy + y²)

Question 3.
4a – 9 + 2b – 6 = 4a – (…….. )

Solution:
4a – 9 + 2b – 6
= 4a – (9 – 2b + 6)

Question 4.
x² -y² + z² + 3x – 2y = x² – (…….. )

Solution:
x² – y² + z² + 3x – 2y
= x² – (y² – z² – 3x + 2y)

Question 5.
– 2a² + 4ab – 6a²b² + 8ab² = – 2a (……… )

Solution:
 – 2a² + 4ab – 6a²b² + 8ab²
= – 2a (a – 2b + 3ab² – 4b²)

Simplify :

Question 6.
2x – (x + 2y- z)

Solution:
2x-(x + 2y-z) = 2x – x – 2y + z
= x – 2y + z

Question 7.
p + q – (p – q) + (2p – 3q)

Solution:
p + q – (p – q) + (2p- 3q)
= p + q – p + q + 2p – 3q = 2p – q

Question 8.
9x – (-4x + 5)

Solution:
9x – (-4x + 5) = 9x + 4x – 5
= 13x- 5

Question 9.
6a – (- 5a – 8b) + (3a + b)

Solution:
6a – (- 5a – 8b) + (3a + b)
= 6a + 5a + 8b + 3a + b
= 6a + 5a + 3a + 8b + b
= 14a + 9b

 Question 10.
(p – 2q) – (3q – r)

Solution:
(p-2q) – (3q – r) =p – 2q – 3q + r =p – 5q + r

Question 11.
9a (2b – 3a + 7c)

Solution:
9a (2b – 3a + 7c)
= 18ab – 27a² + 63ca

Question 12.
-5m (-2m + 3n – 7p)

Solution:
-5m (-2m + 3n- 7p)
= – 5m x (-2m) + (-5m) (3n) – (-5m) (7p)
= 10m² – 15mn + 35 mp.

Question 13.
-2x (x + y) + x²

Solution:
– 2x (x + y) + x²
= -2x x x + (-2x)y + x²
= – 2x² – 2xy + x²
= – 2x² + x² – 2xy = – x² – 2xy

Question 14.

Solution:

Question 15.
8 (2a + 3b – c) – 10 (a + 2b + 3c)

Solution:
8 (2a + 3b -c)- 10 (a + 2b + 3c)
= 16a + 24b – 8c – 10a – 20b- 30c
= 16a – 10a + 24b – 20b – 8c – 30c
= 6a + 4b – 38c

Question 16.

Solution:

Question 17.
5 x (2x + 3y) – 2x (x – 9y)

Solution:
5x (2x + 3y) – 2x (x – 9y)
= 10x² + 15xy – 2x² + 18xy
= 10x² – 2x²+ 15xy+ 18xy
= 8x² + 33 xy

Question 18.
a + (b + c – d)

Solution:
a + (b + c – d) = a + (b + c – d)
= a + b + c – d

Question 19.
5 – 8x – 6 – x

Solution:
5 – 8x – 6 – x
= 5 – 6 –  8x – x
= -1 -7x

Question 20.
2a + (6- \(\overline { a-b }\) )

Solution:
2a + (6 – \(\overline { a-b }\) )
= 2a + (b – a + b)
= 2a + b – a + b
= a + 2b

Question 21.
3x + [4x – (6x – 3)]

Solution:
3x + [4x – (6x – 3)]
= 3x + [4x – 6x + 3]
= 3x + 4x – 6x + 3
= 3x + 4x – 6x + 3
= 7x – 6x + 3= x + 3

Question 22.
5b – {6a + (8 – b – a)}

Solution:
5b- {6a + 8- 6-a}
= 5b – 6a – 8 + b + a
= -6a + a + 5b +b – 8
= -5a + 6b-8

Question 23.
2x-[5y- (3x -y) + x]

Solution:
2x – [5y- (3x – y) + x]
= 2x – {5y – 3x +y + x}
= 2x – 5y + 3x -y – x
= 2x + 3x – x – 5y – y
= 4x – 6y

Question 24.
6a – 3 (a + b – 2)

Solution:
6a – 3 (a + b – 2)
= 6a – 3a – 3b + 6
= 3a -3b + 6

Question 25.
8 [m + 2n-p – 7 (2m -n + 3p)]

Solution:
8 [m + 2n-p -1 (2m – n + 3p)]
8 [m + 2n-p- 14m + 7n-21p]
= 8m+ 16n -8p- 112m + 56n – 168p
= 8m – 112m + 16n + 56n -8p – 168p
= -104m + 72n – 176p

Question 26.
{9 – (4p – 6q)} – {3q – (5p – 10)}

Solution:
{9 – {4p – 6q)} – {3q – (5p – 10)}
{9 – 4p + 6q} – {3q -5p+ 10}
= 9 – 4p + 6q – 3q + 5p – 10
= 9 – 4p + 5p + 6q – 3q – 10
= p + 3q – 1

Question 27.
2 [a – 3 {a + 5 {a – 2) + 7}]

Solution:
2 [a – 3 {a + 5 {a – 2) + 7}]
= 2 [a- 3 {a + 5a- 10 + 7}]
= 2 [a -3a- 15a + 30 -21]
= 2a-6a- 30a + 60-42
= 2a- 36a + 60-42
= -34a + 18

Question 28.
5a – [6a – {9a – (10a – \(\overline { 4a-3a }\)  )}]

Solution:
5a – [6a – {9a – (10a – 4a + 3a)}]
= 5a – [6a – {9a – (10a – 4a + 3a)}]
= 5a – [6a – {9a – 10a + 4a – 3a}]
= 5a- [6a – 9a + 10a – 4a + 3a]
= 5a – 6a + 9a – 10a + 4a – 3a
= 5a + 9a + 4a – 6a – 10a – 3a
= 18a – 19a = – a

Question 29.
9x + 5 – [4x – {3x – 2 (4x – 3)}]

Solution:
9x + 5 – [4x – {3x – 2 (4x – 3)}]
= 9x + 5 – [4x – {3x – 8x + 6}]
= 9x + 5 – [4x – 3x + 8x – 6]
= 9x + 5-4x + 3x-8x + 6
= 9x + 3x-4x-8x + 5 + 6
= 12x- 12x+ 11 = 11

Question 30.
(x + y – z)x + (z + x – y)y – (x + y – z)z

Solution:
(x + y – z)x + (z + x -y )y – (x + y -z)z
= x² + xy – zx + yz + xy -y² – zx – yz + z²
= x² -y² + z² + 2xy – 2zx

Question 31.
-1 [a-3 {b -4 (a-b-8) + 4a} + 10]

Solution:
– 1 [a – 3 {b – 4(a – b – 8) + 4a} + 10]
= -1 [a-3 {b-4{a-b-8) + 4a} + 10]
= -1[a-3 {b-4a + Ab +32 + 4a} + 10]
= -1 [a-3b+ 12a- 126-96- 12a + 10]
= -a + 3b – 12a + 12b + 96 + 12a – 10
= -a-12a + 12a+ 3b+ 12b-96-10
= – a + 15b – 106

Question 32.

Solution:

Question 33.
10 – {4a – (7 – \(\overline { a-5 }\)) – (5a – \(\overline { 1+a }\))}

Solution:

10 – {4a – (7 – \(\overline { a-5 }\)) – (5a – \(\overline { 1+a }\))}
= 10 – {4a – (7 – a + 5) – (5a – 1 – a)}
= 10- {4a -(12 -a) -(4a- 1)}
= 10 – {4a – 12 + a- 4a + 1}
= 10 – 4a + 12 – a + 4a- 1
= 10 + 12 – 1 – 4a – a + 4a
= 21 -a

Question 34.
7a- [8a- (11a-(12a- \(\overline { 6a-5a }\))}]

Solution:
7a – [8a – {1 la – (12a –\(\overline { 6a-5a }\))}]
= 7a-[8a-{11a-(12a-6a + 5a)}]
= 7a -[8a -{11a -(17a -6a)}]
= 7a- [8a- {11a-(11a)}]
= 7a- [8a- {11a- 11a}]
= 7a – 8a = -a

Question 35.

Solution:

Question 36.
x-(3y- \(\overline { 4z-3x }\) +2z- \(\overline { 5y-7x }\))

Solution:
x-(3y- \(\overline { 4z-3x }\) +2z- \(\overline { 5y-7x }\))
= x – (3y – 4z + 3x  + 2z -5y + 7x)
= x-(-2y-2z+10x)
= x + 2y + 2z- 10x
= -9x + 2y + 2z