OP Malhotra Class 12 Maths Solutions Chapter 28 Linear Programming Ex 28(c)

Parents can use S Chand Class 12 Maths Solutions Chapter 28 Linear Programming Ex 28(c) to provide additional support to their children.

S Chand Class 12 ICSE Maths Solutions Chapter 28 Linear Programming Ex 28(c)

Question 1.
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of the first machine is 12 hours and that of second machine is 9 hours. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on the second machine. Each unit of product A is sold at a profit of ₹ 5 and B at a profit of ₹ 6, find the production level for maximum profit graphically.
Solution:
Given data can be arranged in tabular form is as under :

Product	Machine	I	II	Profit (in ₹)
A B		3 2	3 1	5 6
Maximum availability capacity		12	9

Let x units of product A and y units of product B are produced by manufacturer.
Since it is given that each unit of product A is sold at profit of ₹ 5 and that of product B is sold at profit of ₹ 6. Thus the total profit earned by manufacturer is selling x units of product A and y units of product B be 5x + 6y.
Let Z be the total profit ∴ Z = 5x + 6y and our aim is to maximise Z.
and corresponding constraints are :
3x + 2y ≤ 12 (Machine I constraint)
3x + y ≤ 9 (Machine II constraint)
x ≥ 0 ;y ≥ 0 [since no. of units of product A and B can’t be negative]

For region 3x + 2y ≤ 12 ; The line 3x +2y = 12 meets coordinate axes at A (4, 0) and B (0, 6). Since (0, 0) satisfies the given inequality. Thus region containing (0, 0) gives the solution set of given region.
For region 3x +y ≤ 9 ; The line 3x +y = 9 meets coordinate axes at C (3, 0) and D (0, 9). Since (0, 0) lies on given inequality. Thus, the region containing (0, 0) gives the solution set of given region, x ≥ 0, y ≥ 0 represents the first quadrant of XOY plane.

Both lines 3x + 2y = 12 and 3x +y = 9 intersects at P (2, 3). Here the shaded region be the feasible region OCPB and its comer points are O (0, 0) ; C (3, 0) ; P (2,3) and B (0,6). Now we evaluate Z at these comer points.

Corner points	Z = 5x + 6y
O (0,0)	5 × 0 + 6 × s 0 = 0
C (3,0)	5 × 3 + 6 × 0 = 15
P (2,3)	5 × 2 + 6 × 3 = 28
B (0,6)	5 × 0 + 6  × 6 = 36

∴ Z_max = 36 at B (0, 6) i.e. at x = 0 andy – 6 Hence maximum profit of ₹ 36 is earned when 0 units of product A and 6 units of product B are produced.

Question 2.
A diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 calories. Two foods X and Y are available at a cost of ₹4 and ₹3 per unit respectively. One unit of food X contains 200 units of vitamins, 1 unit of minerals and 40 calories while one unit of food 7 contains 100 units of vitamins, 2 units of minerals and 40 calories. Find what combinations of foods A’ and Yshould be used to have least cost, satisfying the requirements.
Solution:
Let x units of food A and y units of food B are used to minimize the cost.
Costs of one unit of food A and B are Rs 4 and Rs 3 per unit respectively, so, costs of x unit of food A and y unit of food B are Ax and 3y respectively. Let Z be total cost,
Then, Z = 4x + 3y
Since one unit of food A and B contain 200 and 100 units of vitamin respectively, So, x units of food A and y units of food a contain 200x and 100y units of vitamin but given minimum requirement of vitamin is 4000 units, so (first constraint) is given by
i.e., 200 + 100y ≥ 4000
2x +y ≥ 40
Since one unit of food A and B contain 1 unit and 3 unit of minerals, so x units of food A and y units of food B contain x and 2y units of minerals respectively but given minimum requirement of minearls is 50 units, so (second constraint) is given by
x + 2y ≥ 50

Since one unit of food A and B contain 40 calories each, so x units of food A and y units of food a contain 40x and 40y calories respectively but given minimum requirement of calories is 1400, so (third constraint) is given by
40x + 40y ≥ 1400 ⇒ x + y ≥ 35
So, required mathematical formulation of LPP is given by
minimize Z = 4x + 3y
Subjects of constraints
2x + y ≥ 40
x + 2y ≥ 50
x + y ≥ 35
x, y ≥ 0 [Since quantity of food can not be less than zero]
Region 2x + y ≥ 40 : Line 2x + y = 40 meets coordinate axes atA₁(20, 0), B₁(0,40). Thus region not containing origin represents the solution set of ineqnation 2x + y ≥ 40 as (0, 0) does not satisfy 2x + y ≥ 40.
Region x + 2y ≥ 50: Line x + 2y = 50 meets axes at C₁(50, 0) and B₂(0,25). Thus region not containing origin represents the solution set of inequation x + 2y ≥ 50 as (0, 0) does not satisfy x + 2y ≥ 50.
Region x + y ≥ 35: Line x + y = 35 meets axes at E₁ (35, 0) and B₃ (0,35). Region not containing origin represents the solution set of inequation x + y ≥ 35 as (0,0) does not satisfy x + y ≥ 35.
The lines x + 2y = 50 and x + y = 35 intersects for at H₁ (20, 15)
The lines 2x + y = 40 and x + y = 35 intersects at G₁ (5, 30)
Region x, y ≥ 0 represents the first quadrant of xy-region.
Unbounded shaded region C₁H₁G₁B₁ represents feasible region with comer points C₁(50,0), H₁(20, 15), G₁(5, 30), B₁ (0, 40);

Corner point	Z = 4x + 3y
C2(50,0)	=4(50) + 3(0) = 200
H1(20,15)	=4(20) + 3(15) = 125
G1(5,30)	=4(5) + 3(30) = 110
B1(0,40)	=4(0) + 3(40) = 120

Smallest value of Z = 110 at x = 5, 30
Since the feasible region is unbounded we want to check whether Z = 110 is minimum or not for this we draw the line 4x + 3y = 110 and check whether the open half plane 4x + 3y < 110 have common points in feasible region.
Open half plane 4x + 3y < 110 has no point in common with feasible region, so, smallest value is the minimum value.

Hence, quantity of food A = x = 5 units
quantity of food B = y = 30 units
and minimum cost = ₹ 110

Question 3.
A small firm manufactures gold rings and chains. The combined number of rings and chains manufactured per day is atmost 24. It takes one hour to make a ring and half an hour for a chain. The maximum number of hours available per day is 16 . If the profit on a ring is ₹ 300 and on a chain ₹ 190, how many of each should be manufactured daily so as to maximize the profit.
Solution:
Let the required number of gold rings and chains manufactured by a firm are x and y respectively to get the maximum profit.
Since, profit on each ring and chains are ₹ 300 and ₹ 190 respectively, so, profit on x units of rings and y units of chains are ₹ 300x and ₹ 190y respectively Let Z be total profit. Then
Z = 300x + 190y
and we have to maximize.
Since each unit of ring and chain require 1 hr and 30 min to make respectively, so, x units of rings and y units of rings require 60x and 30y min. to make respectively, but given iota! time available to make it, is 16 × 60 = 960, so (first constraint) is given by
60x + 30y ≤ 960
Thus, 2x + y ≤ 32
Given, total number or rings and chains manufactured is at most 24, so, second constraint is given by x + y ≤ 24
Hence, the mathematical formulation of given LPP is given below:
Maximum Z = 300x + 190y
Subject to constraints,
2x + y ≤ 32
x + y ≤ 24
x, y ≥ 0 [Since production can not be less than Zero]

Region 2x +y ≤ 32 : The line 2x +y = 32 meets coordinate axes at C(16,0) & D(0,32) respectively.
Region containing origin represents the solution set of 2x +y ≤ 32 as (0,0) satisfies 2x +y ≤ 32.
Region x + y ≤ 24 : line x + y = 24 meets coordinate axes at A(24,0) & B(0, 24) respectively.
Region containing origin represents the solution set of x + y ≤ 24 as (0,0) satisfies x + y ≤ 24.
Region x, y ≥ 0 : it represents the first quadrant of xy-plane.
Thus Shaded region OCEB represents feasible region.
The point E(8, 16) is obtained by solving 2x + y = 32 and x + y = 24 simultaneously.

Corner Point	Z = 300x + 190y
O (0,0)	300(0) + 190(0) = 0
C (16,0)	300(16) + 190(0) = 4800
E (8,16)	300(8) + 190(16) = 5440
B (0,24)	300(0) + 190(24) = 4560

∴ Z_max or maximum Z = 5440 at x = 8, y = 16
∴ reqd. number of rings = 8 and reqd. no. of chains = 16 and maximum profit = ₹ 5440

Question 4.
If a young man rides his motor cycle at 25 km/hr, he has to spend ₹2 per km on petrol, if he rides at a faster speed of 40 km/hr, the petrol cost increases to ₹5 per km. He has ₹100 to spend on petrol and wishes to find maximum distance he can travel within one hour. Express this as a linear programming problem and then solve it.
Solution:
Let the youngman drives his scooter x km at a speed of 25 km/hr and y km at a speed of 40 km/hr.
Let Z be the total distance travelled by him,
Then Z = x + y
Since he spend X 2 per km on petrol when speed is 25 km/hr and ₹ 5 per km on petrol when speed is 40 km/hr, so, expence on x km and y km are ₹ 2x and ₹ 5y respectively, but given he has only X 100. Then (first constraint) is given by
2x + 5y ≤ 100
Time taken by young man to travel x km = \(\frac{\text { Distance }}{\text { speed }}\) = \(\frac{x}{25}\)hr
Time by young man to travel y km = \(\frac{x}{25}\)hr
Given he has 1 hr to travel, Then (second constraint) is given by
\(\frac{x}{25}\) + \(\frac{y}{40}\)hr ≤ 1
⇒ 40x + 25y ≤ 1000
⇒ 8x + 5y ≤ 200
Hence the required mathematical formulation of LPP is given below :
Maximize Z = x + y
subject to constraints,
2x + 5y ≤ 100
8x + 5y ≤ 200
x, y ≥ 0 [Since distance can not be less than zero]
Region 2x + 5y ≤ 100 : line 2x + 5y= 100 meets coordinate axes at A₁ (50, 0) and B₁ (0, 20) respectively,
Region containing origin represents the solution set of 2x + 5y ≤ 100 as (0,0) satisfies 2x + 5y ≤ 100.
Region 8x + 5y < 200 : line Sx + 5y = 200 meets coordinate axes at A₂ (25,0) and B₂(0,40) respectively.
Region containing origin represents the solution set of 8x + 5y ≤ 200 as (0,0) satisfies 8x + 5y ≤ 200.
Region x, y ≥ 0 : it represent the first quadrant of the region.
The point \(\mathrm{P}\left(\frac{50}{3}, \frac{40}{3}\right)\) is obtained by solving 8x + 5y = 200, 2x + 5y = 100 simultaneously

Maximum Z = 30 at x = \(\frac{50}{3}\), y = \(\frac{40}{3}\)
Distance covered by man travelled at speed of 25 km/hr = \(\frac{50}{3}\)km and at speed of 40 km/hr =\(\frac{40}{3}\)km and maximum distance = 30 km.

Question 5.
Every gram of wheat provides 0.1 g of protein and 0.25 g ofcajbohydrates. The corresponding values for rice are 0.05 g and 0.5 g respectively. Wheat costs ₹ 4 per kg and rice ₹ 6 per kg. The mimum daily requirements of protein and carbohydrates for an average child are 50 g and 200 g respectively. In what quantities should wheat and rice be mixed in the daily diet so as to provide the maximum daily requirements of protein and carbohydrates at minimum cost?
Solution:
Given data can be tabulated is as given below :

	Proteins	carbohydrates
Wheat Rice	0.1 g 0.05 g	0.25 g 0.5 g
Minimum daily requirement	50 g	200 g

Let x gm of wheat and y gm of rice be mixed in daily diet to provide the minimum daily requirement of proteins and carbohydrates be required to minimise the cost.
It is given that wheat costs ₹ 4 and rice costs ₹ 6 per kilogram i.e. wheat costs ₹ \(\frac{4}{1000}\) and rice
costs ₹ \(\frac{6}{1000}\) per gram.
So costs of x gm of wheat be ₹ \(\frac{4x}{1000}\) and costs of y gm of rice be₹ \(\frac{6y}{1000}\) .Let Z be the total cost.
Then Z = \(\frac{4x}{1000}\) + \(\frac{6y}{1000}\) and we want to minimise Z.
Thus, the mathematical formulation of gien L.P.P using table is given as under :
Min. Z = \(\frac{4x}{1000}\) + \(\frac{6y}{1000}\)

Subject to constraints;
0.1 x + 0.05y ≥ 50 ⇒ 2x + y ≥ 1000
and 0.25 x + 0.5y ≥ 200 ⇒ x + 2y ≥ 800
x ≥ 0 ; y ≥ 0 [Since quantity of wheat and rice cant be negative]

To solve LPP, we convert the given inequations into eqns :
2x + y = 1000 and x + 2y = 800
We draw the given lines and shaded the region satisfied by all inequations :
The line 2x + y < 1000 meets coordinate axis at A (500, 0) and B (0, 1000)
The line x + 2y = 800 meets coordinate axis at C (800, 0) and D (0, 400) both lines intersects at P (400, 200).
The shaded region OAPD represents feasible and bounded region with comer points O (0, 0) ; A (500, 0); P (400, 200) and D (0, 400).
We evaluate Z at these points

∴ Z_min = 2.8 at x = 400 ; y = 200
So required quantity of wheat = 400 gm
and required quantity of rice = 200 gm
A balanced diet which contains all nutrients in proper quantity. Balanced diet protect us against dieseases. Values promoted are how to make life healthy.

Question 6.
Two tailors A and B earn ₹ 150.00 and ₹200.00 per day respectively. A can stitch 6 shirts and S 4 pants while B can stitch 10 shirts and 4 pants per day. How many days shall each work if it is desired to produce (at least) 60 shirts and 32 pants at a minimum labour cost ?
Solution:
Suppose tailor A and B work for x and y days respectively to minimise the cost.
Since tailor A and B earn ₹ 150 and ₹ 200 respectively So, tailor A and B earning for x and y days be ₹ 15x and 20y respectively, let Z denote maximum profit that gives minimum labour cost Then
Z = 150x + 200y
Since, Tailor A and B stitch 6 and 10 shirts respectively in a day, Thus tailor A can stitch 6x and B can stitch 10y shirts in x and y days respectively, but it is desired to produce 60 shirts at least. Then (first constraint) is given by
6x + 10y ≥ 60
3x + 5y ≥ 30
Since, Tailor A and B stitch 4 pants per day each, so tailor A can stitch 4x and B can stitch 4y pants in x and y days, respectively, but it is desired to produce at least 32 pants, Then (second constraint) is given by
4x + 4y ≥ 32
x +y ≥ 8
Hence, The required mathematical formulation of LPP is, as given below
Min. Z = 150x + 200y
Subject to constraints,
3x + 5y ≥ 30
x + y ≥ 8
x, y ≥ 0 [Since x and y not be less than zero]
Region 3x + 5y ≥ 30: line 3x + 5y = 30 meets coordinate axes at A₂(10,0) and B₂(0,6) respectively. Region not containing origin represents the solution set of inequation 3x + 5y ≥ 30, as (0,0) does not satisfy 3x + 5y ≥ 30.
Region x + y ≥ 8: line x + y = 8 meets axes at C₁(8,0) and D₁(0,8) respectively. Region not containing origin represents the solution set of inequation x + y ≥ 8 as (0,0) does not satisfy x+y ≥ 8.
Region x, y ≥ 0 : it represent the first quadrant in the xy plane, both given lines 3x + 5y = 30 and x + y = 8 intersects at E₁(5, 3).

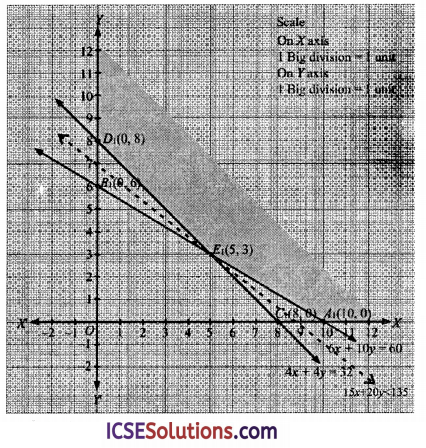
Unbounded shaded region A₁E₁D₁ represents the feasible region with comer points A₁(10,0), E₁(5, 3) and D₁(0.8).

Corner Point	Z = 150x + 200y
A1(10,0)	150(10) + 200(0) = 1500
E1(5,3)	150(5) + 200(3) = 1350
D1(0,8)	150(0) + 200(8) = 1600

Smallest value of Z is 1350, Since the feasible region is unbounded. We have to deck whether the value of Z i.e. 1350 is minimum or not. For this we draw a line 15x + 20y = 135 and check whether the open half plane 15x + 20y < 135 have common points in feasible region or not. Now open half plane 15x + 20y < 135 has no point in common with feasible region, so smallest value is the minimum value. So, Z_min = 1350, at x = 5, y = 3

Thus, Tailor A should work for 5 days and B should work for 3 days.

Question 7.
A dealer wishes to purchase a number of fans and sewing machines. He has only ₹ 57,600 to invest and has space for at most 20 items. A fan costs him 73600 and a sewing machine ₹ 2400. He expects to sell a fan at a profit of ₹ 220 and a sewing machine at a profit of ₹ 180. Assuming that he can sell all the items that he buys, how should he invest his money to maximize the profit ? Solve graphically and find the maximum profit.
Solution:
Let x be the number of fans and y be the no. of sewing machines since it is given that the dealer earns a profit of ₹ 220 on each fan and profit of ₹ 180 on each sewing machine. Thus total profit earn by dealer in selling x units of fans and y units of sewing machines be ₹ (220x + 180y). Let Z be the total profit of dealer.
∴ Z = 220x + 180y and our aim is to maximise Z.
Also he has a space for atmost 20 items. Thus corresponding constraint be x + y ≤ 20
Since the cost of one fan and one sewing machine be ₹ 3600 and ₹ 2400. Thus total cost of x fans and sewing machines be ₹ (3600x + 2400y). Also he has only ₹ 57600 to invest.
∴ 3600x + 2400y ≤ 57600 ⇒ 3x + 2y ≤ 48
Thus the mathematical modeling of given L.P.P be as under Max Z = 220x + 180y
subject to constraints ; x + y ≤ 20
3x + 2y ≤ 48
and x ≥ 0, y ≥ 0
[since the no. of fans and sewing machines can’t be negative]

For region x + y ≤ 20 ; The line x + y = 20 meets coordinate axes at A (20, 0) and B (0, 20). The point (0,0) lies on given region. Thus region containing (0, 0) gives the solution set of given region.
For region 3x + 2y ≤ 48 ; The line 3x + 2y = 48 intersects coordinate axes at C (16, 0) and D (0, 24).
Also (0, 0) lies on given region. Thus, region containing (0,0) gives the solution set of given region.
Also x ≥ 0 and y ≥ 0 represent the first quadrant of XOY plane.
Both lines x + y = 20 and 3x + 2y = 48 intersects at P (8, 12).
Thus the shaded region OCPB represents the feasible region and it is bounded.
and its comer points are O (0,0); C (16,0); P (8,12) and B (0,20).
We evaluate Z at these comer points.

Corner points	Z = 220x + 180y
O (0,0)	0
C (16,0)	220 × 16 + 180 × 0 = 3520
P (8,12)	220 × 8 + 180 × 12 = 1760 + 2160 = 3920
B (0,020)	220 × 0 + 180 × 20 = 3600

∴ Z_max = 3920 at P (8, 12) i.e. at x = 8 and y = 12.
So dealer should sell 8 fans and 12 sewing machine to earn maximum profit.

Question 8.
The Principal of a school wants to buy some geometry boxes and some pocket dictionaries for giving prizes to 15 children. He wants to buy at least four of eachl A geometry box costs 5 whereas a pocket dictionary costs ₹ 10. How many of each should he buy so that expenditure does not exceed ₹ 100 and at the same time he can buy the largest number of prizes.
Solution:
Let x be the number of geometry boxes and y be the no. of pocket dictionaries.
Since it is given that geometry box costs ₹ 5 and a pocket dictionary costs ₹ 10. Thus
Total cost of x geometry boxes and y pocket dictionaries be equal to 5x + 10y and it is given that expenditure does not exceed ₹ 100.
Thus corresponding constraint be 5x + 10y ≤ 100 since he want to buy atleast 4 geometry boxes and four pocket dictionaries.
Thus x ≥ 4 and y ≥ 4.
Let Z be the total number of prizes.

∴ Z = x + y and our aim is to maximise Z. Thus the mathematical modelling of given L.P.P is max Z = x + y.
Subject to constraints ; 5x + 10y ≤ 1co i.e. x + 2y ≤ 20 ; x ≥ 4 and y ≥ 4
The region x + 2y ≤ 20 ; The line x + 2y = 20 meets coordinate axes at A (20, 0) and B (0, 10).
Since (0, 0) satisfies the region and hence region containing (0, 0) gives the soln. set of given region.
For region x ≥ 4 : The line x = 4 is || toy-axis and passes through C (4,0) and since (0,0) does not lies on x ≥ 4. Thus region not containing (0, 0) gives the solution set of given region.
For region y ≥ 4 : The line y = 4 is parallel to x-axis and passing through D (0, 4). Since (0, 0) does not satisfies y ≥ 4. Thus, the region not containing (0, 0) gives the soln. set of given region.
The line x + 2y = 20 and line x = 4 intersects at Q (4, 8).
The line x + 2y = 20 and line y = 4 intersects at R (12, 4).
The lines x = 4 and y = 4 intersects at P (4, 4).
Here, the shaded region PQR be the feasible region and it is bounded.
We evaporate Z at corner points P (4, 4); Q (4, 8) and R (12, 4).

Corner points	Z = x + y
P (4,4)	4 + 4 = 8
Q (4,8)	4 + 8 = 12
R (12,4)	12 + 4 = 16

∴ Z_max = 16 at x = 12 and y = 4
Hence the required no. of geometry boxes be 12 and pocket dictionaries be 4.

Question 9.
Kellogg is a new cereal formed of a mixture of bran and rice that contains at least 88 g of protein and at least 36 mg of iron. Knowing that bran contains 80 g of protein and 40 mg of iron per kg, and that rice contains 100 g of protein and 30 mg of iron per kg, find the minimum cost of producing this new cereal if bran costs ₹5 kg and rice costs ₹4 per kg.
Solution:
Let required quality of bran and rice be x kg y kg in cereal to minimise the cost of cereal.
Given costs of one kg of bran and rice are ₹ 5 and 4 per kg. So, costs of x unit of bran and y kg or rise are 5x and Rs 5y respectively,
and Let total cost of bran and rice be Z,
Then Z = 5x + 4y
Since one kg of bran and rice contain 80 mg and 100 mg of protein. Then,
x kg of bran and y kg of rice contain 80x and 100y grms of protein respectively, but given minimum requirement of proten for keiloggs is 88 gins. Then (first constriant) is given by
80x + 100y ≥ 88 ⇒ 20x + 25y ≥ 22
Since one kg of bran and rice contan 40 mg and 30 mg of iron so,
x kg of bran and y kg of rice contain 40x and 30y mg of iron respectively, but given minimum requirement of iron is 36 mg for keiloggs, so (second constraint) is given by 40x + 30y ≥ 36
Hence, the required mathematical formulation of LPP is, given by
Min. Z = 5x + 4y
subject to constraints,
20x + 25y ≥ 22
40x + 30y ≥ 36
x, y ≥ 0 [Since quantity of bran and rice can not less than zero]

Region 20x + 25y ≥ 22 : line 20x + 25y = 22 meets axes at \(\mathrm{A}\left(\frac{11}{10}, 0\right)\), \(\mathrm{B}\left(0, \frac{22}{25}\right)\) respectively.

Region not containing origin represents the solution set of inequation 20x + 25y ≥ 22 as (0,0) does not satisfy 20x + 25y ≥ 22.
Region 40x + 30y ≥ 36; The line 40x + 30y = 35 meets axes at \(C\left(\frac{9}{10}, 0\right)\), \(\mathrm{D}\left(0, \frac{6}{5}\right)\).
containing origin represents the solution set of inequation 40x + 30y ≥ 36 as (0,0) does not satisfy 40x + 30y ≥ 36.
Also both lines 20x + 25y = 22 and 40x + 30y = 36 intersects at \(\mathrm{E}\left(\frac{3}{5}, \frac{2}{5}\right)\).
So the shaded area AED gives the feasible region which is unbounded.
The value of Z at these comer points is tabulated as under:

Smallest value of Z is 4.6 Now we want to check whether smallest value of Z is minimum or not. For this, we draw the line 5x + 4y = 4.6 and check the open half plane. 5x + 4y < 4.6 home common points in feasible region or not. Now open half plane 5x + 4y < 4.6 has no point in common with feasible region so, smallest value Z is the minimum value. Hence,
Minimum cost of mixture = ₹ 4.6.

Question 10.
A manufacturer makes two products A and B. Product A sells at ₹200 each and takes \(\frac { 1 }{ 2 }\) hour to make. Froduct 3 sells at ₹ 300 each and takes one hour to make. There is a permanent order for 14 numbers of product A and 16 numbers of product B. A working week consists of 60 hours of production and the weekly turnover must not be less than ₹ 10,000.
If the profit on each of product A is ₹ 20 and product B ₹30 then how many of each should be produced so that the profit is maximum? Also, find the profit.
Solution:
Let the number of product A and B be required to maximize profit be x and y respectively. Since, profit on each product A and B are ₹ 20 and ₹ 30 respectively. Then x number of product A and y number of product B gain profits of ₹ 20x and ₹ 30y respectively. Let Z be the total profit then Z = 20x + 30y we have to maximize Z. Since selling prices of each product A and B are ₹ 200 and ₹ 300 respectively. Then revenues earned by selling x and y units of A and B respectively are 200x and 300y but given weekly turnover must not be less than ₹ 10000, so (first constraint) is given by
200x + 300y ≥ 10000 ⇒ 2x + 3y ≥ 100

Since, it is given that, each product A and B requires \(\frac { 1 }{ 2 }\)hr arid 1 hr. to make. So, x units of product A and y units of product B needed \(\frac { 1 }{ 2 }\) x and y hrs. to make respectively but given working time available is maximum 40 hrs. so, (second constraint) is given by
\(\frac { 1 }{ 2 }\) x + y ≤ 40 i.e. x + 2y ≤ 80

There is a permanent order of 14 and 16 of product A and B respectively, Then (third and fourth constraint) is given by
x ≥ 14
y ≥ 16
Hence the mathematical formulation of LPP is, given below :
Z = 20x + 30y
Subject to constraints,
2x + 3y ≥ 100
x + 2y ≤ 80
x ≥ 14
y ≥ 16
x, y ≥ 0 [Since production can not be less than zero]
Region 2x + 3y ≥ 100 : The line 2x + 3y = 100 meets coordinate axes at C₁(50,0) & D₁\(\left(0, \frac{100}{3}\right)\) respectively. Region not containing origin represents the solution set of 2x + 3y ≥ 100 as (0,0) does not satisfy 2x + 3y ≥ 100.

Region x + 2y ≥ 80 : The line x + 2y = 80 meets coordinate axes at A₂(80,0) & B₂(0,40) respectively. Region containing origin represents the solution set of x + 2y ≤ 80 as (0,0) satisfies x + 2y ≤ 80.
Region x ≥ 14 : 3x = 14 is parallel to y-axis and meets x-axis at A₃(14,0)
Region not containing origin represents the solution set of x ≥ 14 as (0,0) does not satisfiy x ≥ 14.
Region y ≥ 16 : The line y = 16 is parallel to x-axis and meets y-axis at B₃ (0,16), Region not containing origin represents the solution set of y ≥ 16 as (0,0) does not satisfy y ≥ 16.

Shaded region E₁F₁G₁H₁ represents the feasible region. Point E₁ (26, 16) is obtained by solving y = 16 and 2x + 3y = 100, simulateously. E₁(48, 16) is obtained by solving y = 16 and x + 2y = 80. On solving x = 14 and x + 2y = 80 we get the point of inter-section be G₁ (14, 33). Also, the point H₁ (14, 24) is obtained by solving x = 14 and 2x + 3y = 100

Corner point	Z = 20x + 30y
E1(26,16)	20(26) + 30(16) = 1000
F1(48,16)	20(48) + 3(16) = 1440
G1(14,33)	20(14) + 3(33) = 1270
H1(14,24)	20(14) + 3(24) = 1000

maximum Z = 1440 at x = 48, y = 16
reqd. Number of product A = 48 and reqd. no. of product B = 16
and maximum profit = ₹ 1440

Question 11.
In my school scholarship is to be given to the students of classes 11 and 12. The class teacher of 11 th class said at least 5 students of his class should get the scholarship and the class teacher of 12th class saicHhat at least 4 students of his class should get the scholarship. Each student of 11th class has to get ? 30 per month whereas each student of 12th class has to get ₹40 per month. The total number of students should be at least 10 but not more than 15. How many students of each class should be selected for the scholarship so as to (i) minimize (ii) maximize the amount for the scholarship.
Solution:
Let x be the required no. of students in class 11th and y be the required no. of students in class 12th, who are selected for scholarship.
Let Z be the total am ount of scholarship. ∴ Z = 30x + 40y
Since each student of class 11th and 12th got ₹ 30 and ₹ 40 per month and our aim is to minimise or maximise Z.
Since it is given that atleast 5 students of class 11th and atleast 4 students of class 12th got the scholarship.
Thus corresponding constraints are x ≥ 5 ;y ≥ 4.
Also, total no. of students should be atleast 10 but not more than 15. ∴ 10 ≤ x + y ≤ 15.
The mathematical modeling of the given L.P.P is as under :
Min Z = 30x + 40y
Subject to constraints ; x ≥ 5 ;y ≥ 4 ; x + y ≥ 10 ; x + y ≤ 15
For region x ≥ 5 ; The line x = 5 is parallel to y-axis and passes through the point A (5, 0).
Since (0, 0) does not satisfies the given region x ≥ 5.
Thus the region not containing (0, 0) gives the solution set of given region.

For region y ≥ 4 ; The line y = 4 is parallel to x-axis and passes through the point B (0, 4). Since (0, 0) does not lies on y ≥ 4. Hence the solution not containing (0, 0) gives the soln. set of given region.

For region x + y ≤ 10 ; The line x + y = 10 meets coordinate axes at C (10, 0) and D (0, 10). Since (0, 0) does not satisfies the given region. Thus the region not containing (0, 0) gives the soln. set of gi ven region.
For region x + y ≤ 15 ; The line x + y = 15 meets coordinate axes at E (15, 0) and F (0, 15). Since (0, 0) lies on given region. Thus, region not containing (0, 0) gives the soln. set of given region.
The line y = 4 meets the line x + y = 10 at P (6, 4).
The line x = 5 meets the line x + y = 10 at Q (5, 5).
The lines x = 5 and x + y = 15 intersects at R (5, 10).
The lines y = 4 and x + y = 15 intersects at S (11, 4).
The shaded region PQRS be the feasible region and bounded.
We calculate Z at comer points P (6, 4); Q (5, 5); R (5, 10) and S (11,4)

Corner points	Z = 30x + 40y
P(6,4)	30 × 6 + 40 × 4 = 320(Min)
Q(5,5)	30 × 5 + 40 × 5 = 350
R(5,10)	30 × 5 + 40 × 10 = 550(Max)
S(11,4)	30 × 11 + 40 × 4 = 480

∴ Z_min = 320 at x = 6 and y = 4 and Z_max = 550 at x = 5 and y = 10

Question 12.
A farmer decides to plant up to 10 hectares with cabbage and potatoes. He decided to grow at least 2, but not more than 8 hectares of cabbage and at least 1, but not more than 6 hectares of potatoes. Let us assume that he makes a profit of ₹ 1500 per hectare on potatoes and ₹ 2000 per hectare on cabbage. How should he plan his farming so as to get the maximum profit? (Assume that all the yield that he gets is sold).
Solution:
Let the farmer decides to plant up to y hectares for cabbage and x hectares for potatoes.
Since it is given that farmer makes a profit of ₹ 1500 per hectare on potatoes and ₹ 2000 per hectare on cabbage. Thus the total profit gained by farmer in x hectares for potatoes and y hectares for cabbage be ₹ (1500x + 2000y).
Let Z be the total profit of farmer.
Then Z = 1500x + 2000y and our aim is to maximise Z.
Since it is given that farmer decided to grow atleast 2 but not more than 8 hectares of cabbage.
∴ Corresponding constraint be 2 ≤ y ≤ 8
Also, it is given that farmer decided to grow atleast 1 but not more than 6 hectares of potatoes. Thus corresponding constraint is 1 ≤ x ≤ 6
Also farmer decides to plant up to 10 hectares with cabbage and potatoes. ∴ x + y ≤ 10
Thus the mathematical modeling of given L.RP is as under : Max Z = 1500x + 2000y
Subject to constraint;
x + y ≤ 10
1 ≤ x ≤ 6
and 2 ≤ y ≤ 8
For region x +y ≤ 10 ; The line x + y = 10 meets coordinate axes at A (10, 0) and B (0, 10) and (0, 0) satisfies given region. Thus region containing (0, 0) gives the soln. set of given region. For region 1 ≤ x ≤ 6 ; The lines x = 1 and x = 6 are parallel to y-axis. The line x = 1 pass through C (1, 0) and line x = 6 pass through D (6, 0). Since (0, 0) lies on x ≤ 6 and solution containing (0, 0) gives the soln. set of given region x ≤ 6.
Also (0, 0) does not lies on region x ≥ 1. Thus region not containing (0, 0) gives the soln. set of x ≥ 1.

For region y ≥ 2 ; The line y = 2 parallel to x-axis and pass through E (0, 2). Since (0, 0) does not lies on y ≥ 2. Thus region not containing (0, 0) gives the soln. set of given region.
For region y ≤ 8 ; The line y = 8 parallel to x-axis and pass through F (0, 8). Since (0, 0) lies on y ≤ 8. Thus region containing (0, 0) gives the soln. set of y ≤ 8.

The lines x = 1
and y = 2 intersects at P (1, 2)
The lines x = 6
and y = 2 intersects at Q (6, 2)
The lines x = 6
and x + y = 10 intersects at R (6, 4)
The lines x + y = 10
and y = 8 intersects at S (2, 8)
The lines x = 1
and y = 8 intersects at T (1, 8)
Thus should region PQRST represents the bounded feasible region and its corner points are P (1, 2) ;
Q (6, 2); R (6, 4), S (2, 8) and T (1,8).

Corner points	Z = 1500x + 2000y
P (1,2)	1500 × 1 + 2000 × 2 = 5500
Q (6,2)	1500 × 6 + 2000 × 2 = 13000
R (6,4)	1500 × 6 + 2000 × 4 = 17000
S (2,8)	1500 × 2 + 2000 × 8 = 19000
T (1,8)	1500 × 1 + 2000 × 8 = 17,500

∴ Z_max = ₹ 19000 at x = 2 and y = 8
Thus the fanner should plan his farming as 2 hectares of potatoes and 8 hectares of cabbage to get maximum profit of ₹ 19000.

Question 13.
A company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is ₹50 each on type A and ? 60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
Solution:
Let number of toys of type A and B produced are x and y respectively to maximise the profit. Since, profits on each unit of toys A and B ₹ 50 and ₹ 60 respectively, so, profits onx units of toys A and y units of toy B are ₹ 50x and ₹ 60y respectively. Let Z be total profit.
Then Z = 50x + 60y
Since each unit of toy A and toy B require 5 min and 8 min for cutting. So x units of toy A andy units of toy B require 5x and 8y min, respectively but given maximum time available for cutting 3 × 60 = 180 min. so (first constraint) is given by
5x + 8y ≤ 180
Since each unit of toy A and toy B require 10 min and 8 min for assembling. So, x units of toy A and y units of toy B require 10x and 8y for assembling respectively but given maximum time available for assembling is 4 × 60 = 240 min, so (Second constraint) is given by
10x + 8y ≤ 240
i.e. 5x + 4y ≤ 120
Hence the mathematical formulation of LPP is given below :
maximize Z = 50x + 60y
Subject to constraints,
5x + 8y ≤ 180
5x + 4y ≤ 120
x, y ≥ 0 [Since production can not be less than zero]
Region 5x + 8y ≤ 180 : The line 5x + 8y = 180 meets coordinate axes at A₁(3 6,0) and B₁\(\left(0, \frac{45}{2}\right)\) respectively.
Region containing origin represents the solution set of 5x + 8y ≤ 180 as (0,0) satisfies 5x + 8y ≤ 180,.

Region 5x + 4y ≤ 120: The line 5x + 4y = 120 meets coordinate axes at C₁(24,0) and D₁(0,30) respectively.
Region containing origin represents the solution set of 5x + 4y ≤ 120, as (0,0) satisfies 5x + 4y ≤ 120.
Region x, y ≥ 0: it represent first quadrant of xy plane.
The shaded region OC₁E₁B₁ represents feasible region.
The point E₁(12,15) is the point of intersection obtained by solving
5x + 8y = 180 and 5x + 4y = 120 simultaneously.

Clearly maximum Z = 1500 at x = 12, y = 15
Thus required Number of toys A = 12, required no. of toys B = 15
and Maximum profit = ₹ 1500

Question 14.
A factory makes cricket bats and hockey sticks. A bat takes 1.5 hours of machine time and 2 hours of craftsman time while a hockey stick takes 2.5 hours of a machine time and 1.5 hours of craftsman time. In a day the factory has available up to 80 hours of machine time and 70 hours of craftsman time. Show that in order to make maximum profit the factory should produce only cricket bats given that the profits on a cricket bat and a hockey stick are ₹ 50 and ₹ 35 respectively.
Solution:
Let the required no. of cricket bat and hockey stick produced by company be x and y respectively. The given data can be arranged in tabular form as under :

Product	Machine time (in hr)	Craftsman (in hr) time	Profit of each product
Cricket bat Hockey stick	1.5 2.5	2 1.5	50 35
Maximum availability	80	70

Since it is given that profit on each cricket bat and on each hockey stick be ₹ 50 and ₹ 35. Thus total profit gained by factory in x bats and y hockey sticks be ₹ (50x + 35y). Let Z be the total profit of factory. Then Z = 50x + 35y and our aim is to maximise Z.
The corresponding (Machine time) constraint is 1.5x + 2.5y ≤ 80.
and craftman time constraint is given by 2x + 1.5y ≤ 70
Thus the mathematical modeling of given L.P.P is as under: Max Z = 50x + 35y
Subject to constraints :
3x + 5y ≤ 160
4x + 3y ≤ 140
x ≥ 0 ; y ≥ 0 [since no of bats and hockey sticks can’t be negative]

For region 3x + 5y ≤ 160 ; The line 3x + 5y = 160 meets coordinate axes at \(\mathrm{A}\left(\frac{160}{3}, 0\right)\) and B (0, 32). since (0, 0) satisfies given region. Thus region containing (0, 0) gives the soln. set of given region.
For region 4x + 3y ≤ 140 ; The line 4x + 3y = 140 meets coordinate axes at C (35, 0) and \(\mathrm{D}\left(0, \frac{140}{3}\right)\), since (0, 0) lies on given region. Thus region containing (0, 0) gives the solution set of given region.
x ≥ 0, y ≥ 0 represents the first quadrant of XOY plane.
Both lines 3x + 5y = 160
and 4x + 3y = 140 intersects at P (20, 20).

Question 15.
A manufacturer produces two types of steel trunks. He has two machines A and B. The first type of trunk requires 3 hours on machine A and 3 hours on machine B. The second type requires 3/hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of ₹30 and ₹25 per trunk of the first type and second type respectively. How many trunks of each type must he make each day to make maximum profit ?
[Note. Same as Solved Ex. 5. There only the Mathematical formulation was required to be determined.]
Solution:
Let the number of steel trunk I and trunk II are required to maximise the profit be x and y respectively.
Since, profit on each trunk I and truck II are ₹ 30 and ₹ 25 respectively, So. profit on x trunk of type I and y trunk of type II are ₹ 30x and ₹ 25y respectively. Let total profit on trunks be Z,
Then Z = 30x + 25y
we have to maximize Z.
Since, each trunk I and trunk II is required to work 3 hrs each on machine A, so, x trunk I and y trunk II is required 3x and 3y hrs respectively to work on machine A but it is given that machine A can work at most 18 hrs, so, (first constraint) is given by
3x + 3y ≤ 18 ⇒ x + y ≤ 6
Since, each trunk I and II is required to work 3 hrs and 2 hrs on machine B, so, x trunk I and y trunk II is required 3x and 2y hrs to work respectively on machine B but it is given that machine B can work for at most 15 hrs. so, (second constraint) is given by 3x + 2y ≤ 15
Hence, The mathematical formulation of LPP is, given below’:
Max Z = 30x + 25y
Subject to constraints,
x + y ≤ 6
3x + 2y ≤ 15
x, y ≥ 0 [Since production of brunk can not be less than zero]
Region x + y ≤ 6 : line x + y = 6 meets coordinate axes at A₁(6,0) & B₁(0,6) respectively. Region containing origin represents the solution set of x + y ≤ 6, as (0,0) satisfies x + y ≤ 6.
Region 3x + 2y ≤ 15 : line 3x + 2y = 15 meets coordinate axes at C₁(5,0) & D₁\(\left(0, \frac{15}{2}\right)\) respectively. Region containing origin represents the solution set of 3x + 2y ≤ 15 as (0,0) satisfies 3x + 2y ≤ 15.

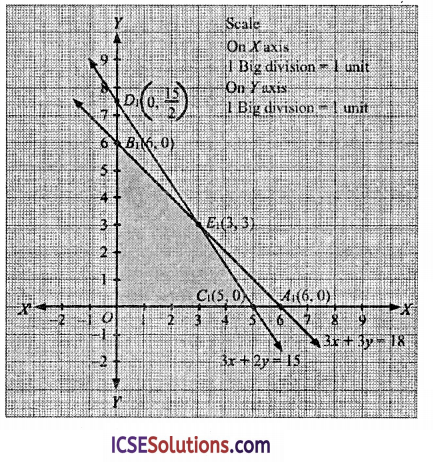
Region x, y ≥ 0 : it represents the first quadrant of 17-plane.
Shaded region OC₁E₁B₁ represents the feasible region. The point E₁(2, 3) is obtained by solving x + 7 = 6 and 3x + 2y = 15 simultaneoulsy.

Corner point	Z = 30x + 25y
C1(5,0)	30(5) + 25(0) = 150
E1(3,3)	30(3) + 25(3) = 165
B1(0,6)	30(0) + 25(6) = 150
O(0,0)	30(0) + 25(0) = 0

Hence maximum Z = 165 at x = 3 and y = 3
reqd. no. of Trunk of type A = 3 and reqd. no. type B = 3 and maximum profit = ₹ 165

Question 16.
A small firm manufactures items A and B. The total number of items A and B that it can manufacture ina day is at the most 24. Item A takes one hour to make while item B takes only half an hour. 16 maximum time available per day is 1 6 hours. If the profit on one unit of item A be ₹300 and ie unit of item B be ₹ 160, how many each of each type of items he produced to maximize the profit? Solve the problem graphically.
Solution:
Let x & y be the required No. of items A & B respectively made by firm to maximize the profit. Since it is given that total number of items = 24, Thus, x + y ≤ 24 (total No. of items constraint) Since it is given that 1 hour spend to make an item A and 1/2 hr is required to make item B so for x items and7 items x his and \(\frac{y}{2}\) has are required to make these items and maximum time available per day be 16 hours.
Thus, x + 0.57 ≤ 16 (time constraint)
x, y ≥ 0
The profit on item A and B be ₹ 300 and be ₹ 160. Let Z be the total profit.
Then Z = 300x + 160y (profit function to be maximized)
Region x + y ≤ 24 ;
The line x + y = 24 meets coordinate axes at A₁(24,0) and B₁(0, 24) and (0,0) lies on it.
So region containing (0,0) represents the solⁿ set of x + y ≤ 24.
Region x + 0.5y ≤ 16 :
The line x + 0.5y = 16 meet coordinate axes at A₂(16,0) and B₂(0, 32) and region containing (0,0) represents the sol11 set of given ineqution.
x ≥ 0, y ≥ 0 represents the first quadrant of xoy plane and both lines intersects P(8, 16).

The shaded region feasible region is OA₂PB₁

Corner Point	Value of Z = 300x + 160y
O(0,0)	0
B1(0,24)	3840
A2(16,0)	4800
P(8,16)	4960

Clearly Z_max = 4960 at x = 8; y = 16
The firm must produce 8 items of A and 16 items of B to maximize the profit of ₹ 4960.

Question 17.
Two godowns, A and B, have a grain storage capacity of 100 quintals and 50 quintals respectively. Their supply goes to three ration shops, D, E and F, whose requirements are 60,50 and 40 quintals respectively. The costs of transportation per quintal from the godowns to the shops are given in the following table.

		Cost of transportation (in ₹ per quintal)
To	From	A	B
D E F		6.00	4.00
		3.00	2.00
		2.50	3.00

How should the supply be transported in order that the transportation cost is minimum?
Solution:
Let godown A supply required x and y quintals of grains to the shops D and E respectively. Then, (100 – x – y) will be supplied to shop F.
It is given that the requirement at shop D is 60 quintals since x quintals are transported from godown A. Therefore, the remaining (60 – x) quintals will be transported from godown B.
Similarly, (50 -y) quintals and 40 – (100 – x – y)
= (x + y – 60) quintals will be transported from godown B to shop E and F respectively.
The given problem can be represented diagrammatically as follows :
i.e. x ≥ 0, y ≥ 0
and 100 – x – y ≥ 0
i.e. x ≥ 0 , y ≥ 0
and x + y ≤ 100
Also, 60 – x ≥ 0, 50 – y ≥ 0 and x + y – 60 ≥ 0
Thus, x ≤ 60, y ≤ 50, and x + y ≥ 60

Total transportation cost Z is given by,
Z = 6x + 3y+ \(\frac { 5 }{ 2 }\) (100 – x – y) + 4 (60 – x) + 2 (50 – y) + 3 (x + y – 60)
⇒ Z = 6x + 3y + 250 – 2.5x – 2 – 5y + 240 – 4x + 100 – 2y + 3x + 3y- 180 i.e,
Z = 2.5x + 1.5y + 410
The mathematically modelling of given problem can be formulated as
Minimize Z = 2.5x + 1.5y + 410
Subject to the constraints;
x + y ≤ 100
x ≤ 60
y ≤ 50
x + y ≥ 60
x, y ≥ 0

For region x + y ≤ 100 ; The line x + y = 100 meet coordinate axes at A( 100, 0) and B(0, 100). Also (0,0) satisfies x + y ≤ 100.; Thus the region containing (0.0) gives the solution set of given inequation. For region x ≤ 60 ; The line x = 60 is a line || to y-axis and meeting C(60, 0) and (0, 0) satisfies x ≤ 60. Thus, the region containing (0,0) represents the inequation x ≤ 60.
For region y ≤ 50 ; The line y = 50 is a line || to x-axis meeting y-axis at B2 (0, 50). Also (0, 0) satisfies y ≤ 50. Thus region containing (0, 0) represents the inequation y ≤ 50.
For region x + y ≥ 60 ; The line x + y = 60 meets coordinate axes at C(60, 0) and D(0, 60). Since (0,0) does not lies on x + y ≥ 60. Hence the region not containing (0, 0) be the solution set of x + y ≥ 30.
The line y- 50 and line x + y = 60 intersects at E(10, 50). The line x = 60 and line x + y = 100 intersects at G (60, 40). F(50, 50) be the point of intersection of lines x = 50 and y = 50.
Thus the feasible region be the shaded area CGFE.
The comer points of feasible region are C (60, 0), G(60, 40), F(50, 50) and E(10, 50).
The values of Z at these corner points are follows :

Corner point	Z = 2.5x + 1.5y + 410
C(60,0)	=2.5 × 60 + 1.5 × 0 + 410 = 560
G(60,40)	=2.5 × 60 + 1.5 × 40 + 410 = 620
F(50,50)	=2.5 × 50 + 1.5 × 50 + 410 = 610
E(10,50)	=2.5 × 10 + 1.50 × 50 + 410 = 510 → Minimum

Clearly Z_min = 510 and x = 10 ; y = 50
Thus, the required amount of grain transported from A to D, E, and F is 10 quintals, 50 quintals, and 40 quintals respectively and from B to D, E, and F is 50 quintals, 0 quintals, and 0 quintals respectively.
Thus, the required minimum cost is ₹ 510.

Question 18.
An oil company has two depots, A and B, with capacities of 7000 L and 4000 L respectively. The .company is to supply oil to three petrol pumps D, E, F, whose requirements are 4500 L, 3000 L and 3500 L respectively. The distances (in km) between the depots and the petrol pumps are given in the following table.

		Distance (in Km)
To	From	A	B
D E f		7	3
		6	4
		3	2

Assuming that the transportation cost per km is ₹ 1 per litre, how should the delivery be scheduled in order that the transportation cost is minimum?
Solution:
Let x and y litres of oil be supplied from A to the petrol pumps, D and E. Then (7000 – x – y) litres will be supplied from A to petrol pump F.
Since it is given that, the requirement at petrol pump D is 4500 L. Since x L are transported from depot A, the remaining (4500 – x) L will be transported from petrol pump B.
Similarly, (3000 – y) L and 3500 – (7000 – x – y) = (x + y – 3500) L will be transported from depot B to petrol pump E and F respectively.

The given problem can be represented diagramatically given as follows.
x ≥ 0, y ≥ 0 and (7000 – x – y) ≥ 0
x ≥0, y ≥ 0 and x + y ≤ 7000
i.e. 4500 – x ≥ 0, 3000 – y ≥ 0,
and x + y – 3500 ≥ 0
Thus, x ≤ 4500, y ≤ 3000, and x + y ≥ 3500
Given cost of transporting 10 L of petrol = Re 1
∴ Cost of transporting 1 L of petrol = ₹\(\frac{1}{10}\)

Therefore, total transportation cost is given by,
Z = \(\frac { 7 }{ 10 }\)x x + \(\frac { 6 }{ 10 }\)y + \(\frac { 3 }{ 10 }\)(7000 – x – y) + \(\frac { 3 }{ 10 }\)(4500 – x) + \(\frac { 4 }{ 10 }\)(3000 – y) + \(\frac { 2 }{ 10 }\) (x + y – 3500)
i.e. Z = 30x + 0.1y + 3950
The given problem can be formulated as follows :
Minimize Z = 0.3x + 0.1y + 3950
subject to the constraints,
x + y ≤ 7000
x ≤ 4500
y ≤ 3000
x + y ≥ 3500
x, y ≥ 0
The feasible region determined by the constraints is as follows.
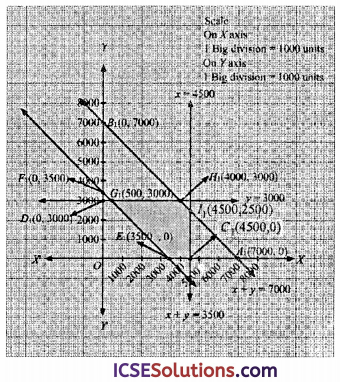
For region x + y ≤ 7000 ; The line x + y = 7000 meets coordinate axes at A₁(7000, 0) and B₁(0, 7000). Region containing (0,0) represents the solution set of inequation.
For region x ≤ 4500; The line x = 4500 is parallel to y-axis meeting x-axis at C₁(4500,0).
Since (0, 0) lies on x ≤ 4500.
Thus region containing (0,0) represents the solution set of inequation x ≤ 4500.
For region y ≤ 3000 ; The line y ≤ 3000 be a line parallel to x-axis and meeting y-axis at D₁(0, 3000). So region containing (0,0) represents the soln set of y ≤ 3000.
Since (0, 0) lies on y ≤ 3000.
For region x + y ≥ 3500 : The line x+y = 3500 meets coordinate axes at E₁(3500, 0) and F₁(0, 3500) since (0,0) does not satisfies and hence region not containing (0,0) represents the solution set of inequation, x, y ≥ 0 represents the first quadrant.
The line x = 4500 meets line x + y = 7000 at I₁(4500, 2500)
and the line y = 3000 meets the line x + y = 7000 at H₁(4000, 3000)
The line y = 3000 meet x + y = 3500 intersects at G₁(500, 3000)
The shaded area E₁C₁I₁H₁G₁ gives the feasible region.
The comer points of the feasible region are E₁(3500,0), C₁(4500,0), I₁(4500, 2500), H₁(4000, 3000) and G₁(500, 3000).

Region x, y ≥ 0 : it represent first quadrant of xy plane.
Shaded region OA₂PB₁ represents feasible region with comer points O(0, 0); A₂(180, 0); P(60, 240) and B₁(0, 300).
The point (60, 240) is obtained by solving x + y = 300 and 2x + y = 360 simultaneously.
The value of objective function at these comer points is given below:

∴ Maximum Z = 1020 at x = 60, y = 240
∴ required number of product A = 60, reqd. no. of product B = 240 and Maximum profit = ₹ 1020

Question 20.
A producer has 30 and 17 units of labour and capital respectively which he can use to produce two types of goods X and Y. To produce one unit of X, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital are required to produce one unit of Y. If Jf and Fare priced at ₹100 and ₹120 respectively, how should the producer use his resources to maximize the total revenue? Solve the problem, graphically.
Solution:
Let required number of goods of type X and Y be x₁ and x₂ respectively.
Since, selling prices of each goods of type X and Y are ₹ 100 and ₹ 120 respectively, so, selling price of x₁ units of goods of type X and x₂ units of goods of type Y are ₹ 100x₁ and ₹ 120x₂ respectively.
Let Z be total revenue,
Then Z = 100x₁ + 120x₂
We want to maximise the total revenue.
Since each unit of goods X and Y require 2 and 3 units of labour, so, x₁ unit of X and x₂ unit of Y require 2x₁ and 3x₂ units of labour units but given maximum labour units available is 30 units, so, (First constraint) is given by
2x₁ + 3x₂ ≤ 30
Since each unit of goods X and Y require 3 and 1 unit of capital so, x₁ unit of X and x₂ unit of Y requires 3x₁ and x₂ units of capital respectively but given maximum units available for capital is 17, so second constriant is given by
3x₁ + x₂ ≤ 17
Hence the mathematical formulation of LPP is given below :
maximize Z = 100x₁ + 120x₂
Subject to constraints,
2x₁ + 3x₂ ≤ 30
3x₁ +x₂ ≤ 17
x₁, x₂ ≥ 0 [Since production of goods can not be less than zero]

Region 2x₁ + 3x₂ ≤ 30; The line 2x₁ + 3x₂ = 30 meets coordinate axes at A(15,0) & B(0,10) respectively. Region containing origin represents the solution set of 2 x₁ + 3x₂ ≤ 30 as (0,0) satisfies 2 x₁ + 3x₂ ≤ 30 as (0,0) satisfies 2x₁ + 3x₂ ≤ 30.

Region 3x₁ + x₂ ≤ 17: The line 3x₁ + x₂ ≤ 17 meet coordinate axes at \(C\left(\frac{17}{3}, 0\right)\), and D(0,17) respectively.

Region containing origin represents the solution set of 3x₁ + x₂ ≤ 17 as (0,0) satisfies 3x₁ + x₂ ≥ 17. Region x₁, x₂ ≥ 0: it represent the first quadrant of x₁ x₂ plane. Thus shaded region OCEB represents the feasible region. The point E(3,8) is obtained by solving 2 x₁+ 3x₂ = 30 and 3x₁ + x₂ = 17 simultaneously.

Clearly maximum Z = 1260 at x = 3, y = 8
∴ Reqd. number of goods of type X = 3, and reqd. of goods of type Y = 8
and maximum profit = ₹ 1260

Question 21.
A farmer has a supply of chemical fertilizer of type I which contains 10% nitrogen and 6% phosphoric acid and type II fertilizer which contains 5% nitrogen and 10 % phosphoric acid. After testing the soil conditions of a field, it is found that at least 14 kg of nitrogen and 14 kg of phosphoric acid is required for a good crop. The fertilizer type I costs ₹ 2.00 per kg and the type II costs ₹ 3.00 per kg. How many kilograms of each fertilizer should be used to meet the requirements and the cost be minimum.
Solution:
Let x kg of fertilizer I and y kg of fertilizer II are used.
The given information can be put in tabular form :

	Type I x	Type II y
Nitrogen phosphoric acid Minimize Cost	0.1 x 0.06 x 2 x	0.05y ≥ 14 0.1y ≥ 14 3y

Our aim is to find the values of x and y that minimize the function Z = 0.6x + 0.4y subject to the constraints
0.1x + 0.05y ≥ 14
0.06x + 0.1y ≥ 14
x, y ≥ 0
converting the given inequations to equations,
0.1x + 0.05y = 14
0.05x + 0.1y = 14
x = 0 = y
For region 0.1x + 0.05y ≥ 14; The line 0.1x + 0.05y ≥ 14 meet coordinate axes at C₁(140, 0) & D₁(0, 280). Region not containing (0,0) represents the solⁿ set of 0.1x + 0.05y ≥ 14 since (0,0) does not lies on it.
For region 0.05y + 0.1y ≥ 14; The line 0.05x + 0.1y = 14 meet coordinate axes at A \(\left(\frac{700}{3}, 0\right)\) and (0, 140) and B(0, 140) and region not containing (0,0) gives the solution set of given inequation. Also, x ≥ 0, y ≥ 0 represents the first quadrant of XOY plane.
Further both lines intersects at E(100, 80) So shaded area AED be the feasible region.

The minimum value of Z = 440 occurs at x = 100, y = 80. Since the region is unbounded.
So, we check whether Z_min = 440 or not. For this, we draw a line 2x + 3y = 440 and check whether open half plane 2x + 3y < 440 have common points in feasible region or not.
Since, there are no common points in feasibie region, so x = 100, y = 80 with a value of 440 is the optimal minimum.

Question 22.
A company produces two types of belts, A and B. Profits on these type are ₹2 and ₹1.5 on each belt, respectively. A belt of type A requires twice as much time as a belt of type B. The company C can produce at the most 1000 belts per day, Material for 800 belts per day is available. At the most 400 buckles for belts of type A and 700 for those of type B are available per day. How many belts of each type would the company produce so as to maximize the profit?
Solution:
Lei required number of belt A and B be x and y and are used to maximise the profit.
Given, profit on belt A and B be ₹2 and ₹ 1.50 per belt, So profit on x belt of type A and y belt to type B be 2x and 1.5y respectively.
Let Z be total profit,
Then Z = 2x + 1.5y
Since is given that each belt of type A requires twice as much time as belt B. Let each belt B require 1 hour to make, so, A requires 2 hours. For x and y belts of type A and B so, it required 2x and y hours to make a but given company produce 1000 belts per day. (first constraint) is given by
2x +y ≤ 1000
Given supply of leather only for 800 belts per day (both A and B combined), so (second constraint) is given by
x + y ≤ 800
given Buckets available for A is only 400 and for B only 700, so, (third constraint) <& (fourth constraint) are given by
x ≤ 400
y ≤ 700
Hence the required mathematical formulation of LPP is, given below
max Z = 2x + 1.5y
subject to constraints,
2x + y ≤ 1000
x + y ≤ 800
x ≤ 400
y ≤ 700
x, y ≥ 0 [Since number of belt can not be less than zero]
Region 2x + y ≤ 1000 : line 2x + y = 1000 meets axes at C₁(500,0), D₁(0, 1000) respectively. Region containing origin represents the solution set of 2x + y ≤ 1000 as (0,0) satisfies 2x + y ≤ 1000. Region x + y ≤ 800 : line x+y = 800 meets axes at A₁(800,0), B₁(0, 800) respectively. Region containing origin represents the solution set of x +y ≤ 800 as (0,0) satisfies x + y ≤ 800.
Region Region x ≤ 400 : line x = 400 be a line parallel to y axis and meet x – axis at E₁(400,0). Region containing origin represents the solution set ofx < 400 as (0,0) satisfies x < 400.
Region Region y ≤ 700 : line y = 700 is parallel to x-axis and meet y-axis at F,(0, 700). Region containing origin represents the solution set of y ≤ 700 as (0,0) satisfies y ≤ 700.
Region x, y ≥ 0 : it represent the first quadrant of the xy plane.

Shaded region OE₁H₁G₁I₁F₁ is feasible region, H₁(400, 200) is point of intersection of 2x+y = 1000 and x = 400 and G₁(200, 600) be the point of intersection of x +y = 800 and 2x +y = 1000. Also, I₁(100 700) be the point of intersection ofy = 700 and x+y = 800.

Corner point	Z = 2x + 1.5y
O(0,0)	2(0) + 1.5(0) = 0
E1(400,0)	2(400) + 1.5(0) = 800
H1(400,200)	2(400) + 1.5(200) = 1100
G1(200,600)	2(200) + 1.5(600) = 1300
l1(100,700)	2(100) + 1.5(700) = 1250
F1(0,700)	2(0) + 1.5(700) = 1050

Therefore, maximum Z or Z_max = 1300, at x = 200, y = 600
Required number of belt A = 200, required no. of belt B = 600
and maximum profit = ₹ 1300.

Question 23.
All oil company requires 12,000, 20,000 and 15,000 barrels of high-grade, medium grade and low grade oil, respectively. Refinery A produces 100,300 and 200 barrels per day of high-grade, medium-grade and low-grade oil, respectively, while refinery 3 produces 200, 400 and 100 barrels per day of high-grade, medium-grade and low-grade oil, respectively. If refinery A costs ₹400 per day and refinery B costs ? 300 per day to operate, how many days should each be run to minimize costs while satisfying requirements.
Solution:
Suppose refineries A and B should run for x and y days respectively to minimize the total cost. The given data can be arranged in tabular form is as under :

Refinery	High grade	Medium grade	Low-grade	Cost per day
A B	100 200	300 400	200 180	₹ 400 ₹ 30
Minimum requirement	12,000	20,000	15,000

It is given that refinery A costs ₹ 400 per day and refinery B costs ₹ 300 per day to operate. So total cost in operating refinery A for x days and refinery B for y days be equal to 400x + 300y and let Z be the total cost in operating refineries A and B. ∴ Z = 400x + 300y and our aim is to minimize Z.

High grade constraint is given by 100x + 200y ≥ 12000 i.e. x + 2y ≥ 120
Medium grade constraint is given by 300x + 400y ≥ 20000 ⇒ 3x + 4y ≥ 200
and Low grade constraint is given by 200x + 100y ≥ 15000 ⇒ 2x + y ≥ 150
Thus, the mathematical modeling of given L.RP is as under :
Min Z = 400x + 300y
Subject to constraints ; x + 2y ≥ 120 ; 3x + 4y ≥ 200 ; 2x + y ≥ 150 ; x, y ≥ 0 [since no. of days can’t be negative]
For region x + 2y ≥ 120 ; The line x + 2y= 120 meets coordinate axes at A (120, 0) and B (0, 60). Since (0, 0) does not satisfies given region. Thus region not containing (0, 0) gives the soln, set of given region.

Foe legion 3x + 4y ≥ 200; The line 3x+4y = 200 meets-axes at \(\mathrm{C}\left(\frac{200}{3}, 0\right)\) and D (0, 50). Since (0,0) does not coordinate satisfies 3x + 4y ≥ 200. Thus the region hot containing (0, 0) gives the soln. set of given region.
For region 2x+y ≥ 150 ; The line 2x + y = 150 meets coordinate axes at E(75, 0) and F (0, 150). Clearly (0,0) does cot -satisfies given region. Thus region not containing (0,0) gives the solution set of given regions Region x, y ≥ 0 represents the first quadrant of XOY plane.
The lines 2x + y = 130
and x + 2y = 120
intersects at P (60, 30).
Thus the shaded region APF represents the unbounded feasible region.
and its corner points are
A (12,0); P (60, 30) and F (0, 150).
We evaluate Z at, these comer points.

Here smallest value of Z be 33000 at P(60, 30).
Since the region is unboxaded. So we check whether smallest value of Z is min or not.
For this, we check open hall plane 400x + 300y < 33000 ⇒ 4x + 3y ≤ 330 have common points in feasible region or not. Clearly open half plane have no common points in feasible region.
∴ smallest value of Z is minimum. ∴ Z_min = 33000 at x = 60 and y = 30.
Hence refinery A and B should run 60 days and 30 days respectively to minimize cost.

Question 24.
A company produces soft drinks that has a contract which requires that a minimum of 80 units of the chemical and 60 units of the chemical B to go into each bottle of the drink. The chemicals are available in a prepared mix from two different suppliers. Supplier S has a mix of 4 units of A and 2 units of B that costs ₹10, the supplier 7 has a mix of 1 unit of A and 1 unit of B that costs ₹4. How many mixes from S and T should the company purchase to honour contract requirement and yet minimize cost?
Solution:
Let x and y units of mixture are purchased from supplier S and T respectively. The given data can be arranged in tabular form is as under :

Since it is given that cost of 1 unit of mixture purchased from supplier S and T be ₹10 and ₹4 respectively. Thus total cost for the company purchasing mixtures of x units of supplier S and y units of supplier T be ₹(10x + 4y). Let Z be the total cost. Then Z = 10x + 4y. Thus our aim is to minimize Z.
The (chemical A) constraint is given by 4x + y ≥ 80
The (chemical B) constraint is given by x + y ≥ 60
Thus the mathematical modeling of given L.P.P is as under :
Min Z = 10x + 4y
Subject to constraints ;
4x + y ≥ 80
2x + y ≥ 60
x,y ≥ 0
[since no. of units can’t be negative]

For region 4x + y ≥ 80 ; The line 4x + y = 80 meets coordinate axes at A (20, 0) and B (0, 80). Since (0, 0) does not satisfies 4x + y ≥ 80. Thus region not containing (0, 0) gives the soln. set of given region.
For region 2x + y ≥ 60 ; The line 2x + y = 60 meets coordinate axes at C (30, 0) and D (0, 60). Since (0,0) does not satisfies given region. Hence the region not containing (0,0) gives the soln. set of given region.
Region x, y ≥ 0 represents the first quadrant of XOY plane. Both lines 4x + y = 80 and 2x + y = 60 intersects at P (10, 40).
The shaded region CPB represents feasible region and feasible region is unbounded and its comer points are C (30, 0); P (10, 40) and B (0, 80) and evaluate Z at these comer points.

Corner points	Z = 10x + 4y
C(30,0)	10 × 30 = 300
P(10,40)	10 × 10 + 4 × 40 = 260
B(0,80)	10 × 0 + 4 × 80 = 320

Here smallest value of Z be 260 at P (10, 40) but region is unbounded so we check this smallest value of Z is minimum or not. For this, we check open half plane 10x + 4y < 260 have common points in feasible region or not. Clearly open half plane have no point common in feasible region.
∴ Z_min = 260 at x = 10 and y = 40
Hence 10 mixtures from supplier S and 40 mixtures from supplier T are required to minimized the cost.

Examples

Question 1.
A manufacturer produces two types of steel trunks. He has two machines, A and B, The first type trunk requires 3 hours on machine A and 3 hours on machine B. The second type requires 3 hours on machine A and 2 hours on machine 6. Machines A and B can work at most for V 18 hours and IS hours per day respectively. He earns a profit of ₹30 per trunk on the first type of trunk and ₹25 per trunk on the second type. Formulate a linear programming problem to find out how many trunks of each type he must make each day to maximize his profit.
Solution:
Let the number of steel trunk I and trunk II are required to maximise the profit be x and y respectively.
Since, profit on each trunk I and truck II are ₹30 and ₹ 25 respectively, So. profit on x trunk of type I and y trunk of type II are ₹30x and ₹25y respectively. Let total profit on trunks be Z,
Then Z = 30x + 25y
we have to maximize Z.

Since, each trunk I and trunk II is required to work 3 hrs each on machine A, so, x trunk I and y trunk II is required 3x and 3y hrs respectively to work on machine A but it is given that machine A can work at most 18 hrs, so, (first constraint) is given by
3x + 3y ≤ 18 ⇒ x + y ≤ 6
Since, each trunk I and II is required to work 3 hrs and 2 hrs on machine B, so, x trunk I and y trunk II is required 3x and 2y hrs to work respectively on machine B but it is given that machine B can work for at most 15 hrs. so, (second constraint) is given by
3x + 2y ≤ 15
Hence, The mathematical formulation of LPP is, given below :
Max Z = 30x + 25y
Subject to constraints,
x + y ≤ 6
3x + 2y ≤ 15
x, y ≥ 0 [Since production of brunk can not be less than zero]

Region x +y ≤ 6 : line x +y = 6 meets coordinate axes at A₁(6,0) & B₁(0,6) respectively. Region containing origin represents the solution set of x + y ≤ 6, as (0,0) satisfies x + y ≤ 6.
Region 3x + 2y ≤ 15 :line 3x + 2y = 15 meets coordinate axes at C₁(5,0) & \(D_1\left(0, \frac{15}{2}\right)\) respectively.
Region containing origin represents the solution set of 3x + 2y ≤ 15 as (0,0) satisfies 3x + 2y ≤ 15.
Region x, y ≥ 0 : it represents the first quadrant of xy-plane.
Shaded region OC₁E₁B₁ represents the feasible region. The point E₁(2,3) is obtained by solving x + y = 6 and 3x + 2y= 15 simuitaneoulsy.

Corner point	Z = 30x + 25y
C1(5,0)	30(5) + 25(0) = 150
E1(3,3)	30(3) + 25(3) = 165
B1(0,6)	30(0) + 25(6) = 150
O(0,0)	30(0) + 25(0) = 0

Hence maximum Z = 165 at x = 3 and y = 3
reqd. no. of Trunk of type A = 3 and reqd. no. type B = 3 and maximum profit = ₹ 165

Question 2.
A new cereal, formed of a mixture of bran and rice, contains at least 88 grams of protein and at east 36 milligrams of iron. Knowing that bran contains 80 grams of protein and 40 milligram of iron per kilogram, and that rice contains 100 grams of protein and 30 milligram of iron per kilogram, find the minimum cost of producing a kilogram of this new cereal if bran costs ₹28 per kilogram and rice costs ₹25 per kiiogram.
Solution:
Let required quality of bran and rice be x kg and y kg in cereal to minimise the cost of cereal.
Given costs of one kg of bran and rice are ₹ 28 and 25 per kg. So, costs of x unit of bran and y kg or rice are 28x and Rs 25y respectively,
and Let total cost of bran and rice be Z,
Then Z = 28x + 25y
Since one kg of bran and rice contain 80 mg and 100 mg of protein. Then,
x kg of bran and y kg of rice contain \(\frac { 80 }{ 1000 }\)x and \(\frac { 100 }{ 1000 }\)y grms of protein respectively, but given minimum requirement of proten for kelloggs is 88 gms. Then (first constriant) is given by
\(\frac { 80 }{ 1000 }\)x + \(\frac { 100 }{ 1000 }\)y ≥ \(\frac { 88 }{ 1000 }\)
⇒ 20x + 25y ≥ 22
Since one kg of bran and rice contains 40 mg and 30 mg of iron so,
x kg of bran and y kg of rice contain 40x and 30y mg of iron respectively, but given minimum requirement of iron is 36 mg for kelloggs, so (second constraint) is given by 40x + 30y ≥ 36
Hence, the required mathematical formulation of LPP is, given by
Min. Z = 5x + 4y
subject to constraints,
20x + 25y ≥ 22
40x + 30y ≥ 36
x, y ≥ 0 [Since quantity of bran and rice can not less than zero]

Region 20x + 25y ≥ 22 : line 20x + 25y = 22 meets axes at \(\mathrm{A}\left(\frac{11}{10}, 0\right)\), \(\mathrm{B}\left(0, \frac{22}{25}\right)\)
Region not containing origin represents the solution set of inequation 20x + 25y ≥ 22 as (0,0) does not satisfy 20x + 25y ≥ 22.
Region 40x + 30y ≥ 36; The line 40x + 30y = 35 meets axes at \(C\left(\frac{9}{10}, 0\right)\), \(\mathrm{D}\left(0, \frac{6}{5}\right)\). Region not containing origin represents the solution set of inequation 40x + 30y ≥ 36 as (0,0) does not satisfy 40x + 30y ≥ 36.

Also both lines 20x + 25y = 22 and 40x + 30y = 36 intersects at \(\mathrm{E}\left(\frac{3}{5}, \frac{2}{5}\right)\)
So the shaded area AED gives the feasible region which is unbounded.
The value of Z at these comer points is tabulated as under:

Smallest value of Z is 4.6 Now we want to check whether smallest value of Z is minimum or not. For this, we draw the line 28x + 25y = 26.80 and check the open half plane. 28x + 25y = 26.80 home common points in feasible region or not. Now open half plane 28x + 25y < 26.80 has no point in common with feasible region so, smallest value Z is the minimum value. Hence, Minimum cost of mixture = ₹ 26.80.

Question 3.
A company produces two types of items, P and Q. Manufacturing of both items requires the metals gold and copper. Each unit of item requires 3 grams of gold and 1 gram of copper while that of item Q requires 1 gram of gold and 2 grams of copper. The company has 9 grams of gold and 8 grams of copper in store. If each unit of item P makes a profit of ₹50 and each unit of item Q makes a profit of ₹60, determine the number of units of each item that the company should produce to maximize profit. What is the maximum profit ?
Solution:
Let number of goods A and B be x and y respectively are required to maximise the profit.
Since, profits on each A and B are ₹ 50 and ₹ 60 respectively. So, profits on x goods of type A and y goods of type B are 50x and 60y respectively,
Let Z be total profit on A and B.
Then Z = 50x + 60y
Since, each A and B require 3 gm and 1 gm of silver respectively. So, x goods of type A and y goods of type B require 3x and y gm silver respectively but, given total silver available is 9gm. So, (first constraint) is given by
3x + y ≤ 9
Since, each goods of type A and B require 1 gm and 2gm of gold respectively, so, x good of type A and y goods of type B require x gm and 2y gm of gold respectively but, given total gold available is 8gm. Then (second constraint) is given by x + 2y ≤ 8
Hence mathematical formulation of LPP is, given below:
Max Z = 50x + 60y
Subject to constraints,
3x + y ≤ 9
x + 2y ≤ 8
x, y ≥ 0 [Since products of A and B can not be less than zero]

Region 3x +y ≤ 9 : Then line 3x +y = 9 meets coordinate axes at A₁(3,0) & B₁(0,9) respectively. Region containing origin respresents the solution set of 3x + y ≤ 9 as (0,0) satisfies 3x + y ≥ 9.
Region x + 2y ≤ 8 : line x + 2y = 8 meets coordinate axes at C₁(8,0) & D₁(0,4) respectively. Region containing origin represents the solution set of x + 2y ≤ 8 as (0,0) satisfies x + 2y ≤ 8.
Region x, y ≥ 0 : it represents first quardant of xy region.
Shaded region OA₁E₁D₁ is the feasible region. The points E₁(2,3) is obtained by solving 3x + y = 9 and x + 2y = 8 simultaneously.
The comer points of feasible region are 0(0, 0); A₁(3, 0); E₁(2, 3) and D₁(0, 40).

Corner point	Z= 50x + 60y
O(0,0)	40(0) + 50(0) = 0
A1(3,0)	50(3) + 60(0) = 150
E1(2,3)	50(2) + 60(3) = 280
D1(0,40)	50(0) + 60(4) = 240

Therefore maximum Z = 280 at x = 2, y = 3
Hence, reqd. Maximum profit = ₹ 230 and required number of goods of type A = 2, and reqd no. of goods of type B = 3.

Question 4.
A manufacturer manufactures two types of tea-cups, A and B. Three machines are needed for manufacturing the tea cups. The time in minutes required for manufacturing each cup on the machines is given below:

Type of cup	Time in minutes
	Machine I	Machine II	Machine III
A B	12 6	18 0	6 9

Each machine is available for a maximum of 6 hours per day. If the profit on each cup of type A is ₹1.50 and that on each cup of type B is ₹1.00, find the number of cups of each type that should be manufactured in a day to get maximum profit.
Solution:
Let the required of tea-cups of type A and B are be x and y respectively.
Since it is given that profits on each tea-cups of type A and B are Rs. 1.50 and Rs. 1.00. Thus, profits on x tea-cups and y tea cups are 1,50x and y respectively. Let Z be the total profit on tea-cups Then Z = 1.50x + 1.00y
We have to maximise Z.
Since, each tea-cup of type A and B require to work on machine 1 for 12 and 6 minute respectively so, x tea-cups of type A and y tea cups of B require to work on machine I for 12x and 6y minutes respectively but given total time available on machine 1 is 6 × 60 = 360 minutes, so, first constraint is given by
12x + 6y ≤ 360
Since, each tea-cup of type A and B require to work machine II for 18 and 0 minute respectively so, x tea-cups of type A and y tea cups of B require to work on machine II for 18x and 0y minutes respectively, but given max Total time available on machine II is 6 × 60 = 360 minutes, so second constraint is given by
18x + 0y ≤ 360
x ≤ 20
Since each tea-cup of type A and B require to work machine III for 6 and 9 minutes respectively so, x tea cups of type A and y tea cups of B require to work on machine III for 6x and 9y minutes respectively given total time available on machine III is 6 × 60 = 360 minutes, so, third constraint is given by
6x + 9y ≤ 360
Hence the required mathematical formulation of LPP is, find x and y which maximize
Z = 1.50x + 1.00y
subject to constrants,
12x + 6y ≤ 360
x ≤ 20
6x + 9y ≤ 360
x,y > 0 [Since production of tea cups can not be less than zero]
Region 12x + 6y < 360 : line 12x + 6y = 360 meets coordinate axes at A₁(30,0) & B₁(0, 60) respectively, Region containing origin represents the solution set of 2x + 6y ≤ 360 as (0,0) satisfies 12x + 6y ≤ 360.

Region x ≤ 20 : line x = 20 is parallel to v-axes and meets x-axes at C₁(20,0). Region containing origin represents the solution set of x ≤ 20 as (0,0) satisfies x ≤ 20.
Region 6x + 9y ≤ 360 : line 6x + 9y = 360 meets coordinate axes at E₁(60,0) & F₁(0, 40) respectively. Region containing origin represents the solution set of 6x + 9y < 360 as (0,0) satisfies 6x + 9y < 360.
Shaded region OC₁H₁G₁F₁ is the feasible region. The point of intersection H₁(20, 20) is obtained by solving x = 20 and 12x + 6y = 360 simultaneously and G₁(15, 30) is the point obtained by solving 12x + 6y = 360 and 6x + 9y = 360 simultaneously.

Corner point	Z = 1.50x + 1.00y
O(0,0)	1.50(0) + 1.00(0) = 0
C1(20,0)	1.50(20) + 1 × (0) = 30
H1(20,20)	1.50(20) + 1(20) = 50
G1(15,30)	1.50(15) + 1(30) = 52.5
F1(0,40)	1.50(0) + 1(40) = 40

Hence, Z is maximum at x = 15, y = 30 and Z_max = 52.5
Thus, 15 teacups of type A and 30 tea-cups type B are needed to maximize profit.

Question 5.
Two tailors P and Q earn Rs. 150 and Rs. 200 respectively. P can stitch 6 shirts and 4 trousers a day, while Q can stitch 10 shirts and 4 trousers per day. How many days should each work to produce at least 60 shirts and 32 trousers at minimum labour cost?
Solution:
Suppose tailor A and B work for x and y days respectively to minimise the cost.
Since tailor A and B earn ₹ 150 and ₹ 200 respectively So, tailor A and B earning for and y days be ₹ 15x and 20y respectively, let Z denote maximum profit that gives minimum labour cost Then
Z= 150x + 200y
Since, Tailor A and B stitch 6 and 10 shirts respectively in a day, Thus tailor A can stitch 6x and B can stitch 10y shirts in x and y days respectively, but it is desired to produce 60 shirts at least. Then (first constraint) is given by
6x + 10y ≥ 60
3x + 5y ≥ 30
Since, Tailor A and B stitch 4 pants per day each, so tailor A can stitch 4x and B can stitch 4y pants in x and y days, respectively, but it is desired to produce at least 32 pants, Then (second constraint) is given by
4x + 4y ≥ 32
x+y ≥ 8
Hence, The required mathematical formulation of LPP is, as given below:
Min. Z= 150x + 200y

Subject to constraints, 3x + 5y ≥ 30
x + y ≥ 8
x, y ≥ 0 [Since x and y not be less than zero]
Region 3x + 5y ≥ 30: line 3x + 5y = 30 meets coordinate axes at A₁(10,0) and B₂(0,6) respectively. Region not containing origin represents the solution set of inequation 3x + 5y ≥ 30, as (0,0) does not satisfy 3x + 5y ≥ 30.
Region x + y ≥ 8: line x + y = 8 meets axes at C₁(8,0) and D₁(0,8) respectively. Region not containing origin represents the solution set of inequation x + y ≥ 8 as (0,0) does not satisfy x + y ≥ 8.
Region x, y ≥ 0 : it represent the first quadrant in the xy plane.
both given lines 3x + 5y = 30 and x +y = 8 intersects at E₁(5, 3).
Unbounded shaded region A₁E₁D₁ represents the feasible region with comer points A₁(10,0), E₁(5, 3) and D₁(0.8).

Corner Point	Z = 150 + 200y
A}_1(10,0)	150(10) + 20(0) = 1500
E}_1(5,3)	150(5) + 200(3) = 1350
D}_1(0,8)	150(0) + 200(8) = 1600

Smallest value of Z is 1350, Since the feasible region is unbounded. We have to deck whether the value of Z i.e. 135 is minimum or not. For this we draw a line 15x + 20y = 135 and check whether the open half plane 15x + 20y < 135 have common points in feasible region or not. Now open half plane 15x + 20y < 135 has no point in common with feasible region, so smallest value is the minimum value. So, Z_min = 1350, at x = 5, y = 3
Thus, Tailor A should work for 5 days and B should work for 3 days.

Question 6.
A mill owner buys two types of machines A and B for his mill. Machine A occupies 1000 sqm of area and requires 12 men to operate it; while machine B occupies 1200 sqm of area and requires 8 men to operate it. The owner has 7600 sqm of area available and 72 men to operate the machines. If machine A produces 50 units and machine B produces 40 units daily, how many machines of each type should he buy to maximise the daily output? Use Linear Programming to find the solution.
Solution:
First of all, we arrange the given data is tabular form is given as under :

Machines	Area (sq. m)	Man-power
A B	1000 1200	12 8
Maximum availability	7600	72

Let the mill owner buys x no. of machines A and y no. of machine B respectively. Since it is given that machine A produces 50 units and machine B produces 40 units daily. Thus total daily output produced by x machines of type A and y machines of type B be (50x + 40y). Let Z be the total output.
Thus, Z = 50x + 40y and our aim is to maximise.
Clearly Area constraint is given by
1000x + 1200y ≤ 7600 ⇒ 5x + 6y ≤ 38
and Man-power constraint is given by
12x + 8y ≤ 72 i.e. 3x + 2y ≤ 18
The mathematical modeling of given L.P.P is as under :
Max Z = 50x + 40y
Subject to constraints ;
5x + 6y ≤ 38
3x + 2y ≤ 18
x, y ≥ 0 [since no. of machines can’t be negative]
For region 5x + 6y ≤ 38 ; The line 5x + 6y = 38 meets coordinate axes at \(\mathrm{A}\left(\frac{38}{5}, 0\right)\) and \(\mathrm{B}\left(0, \frac{19}{3}\right)\) Since (0, 0) satisfies the given region. Thus region containing (0, 0) gives the soln. set of given region.

For region 3x + 2y ≤ 18 ; The line 3x + 2y = 18 meets coordinate axes at C (6,0) and D (0, 9). Since (0, 0) satisfies the given region. Thus, region containing (0, 0) gives the solution set of given region, x, y ≥ 0 represents the first quadrant of XOY plane. Both lines 5x + 6y = 38 and 3x + 2y= 18 intersects at P (4, 3).
Clearly the shaded region OCPB represents the bounded feasible region.
The corner points of feasible region are O(0, 0), C(6, 0); P(4, 3) and B \(\left(0, \frac{19}{3}\right)\).

We evaluate Z at these corner points in tabular form as under :

Here Z_max = 320 at P (4, 3) i.e. at x = 4 and y = 3
Thus the mill owner should buy 4 machines of type A and 3 machines of type B to get maximum daily output.

Question 7.
A company manufactures two types of toys A and B. A toy of type A requires 5 minutes for cutting and 10 minutes for assembling while toy of type B requires 8 minutes for each. There are hours available for cutting and 4 hours available for assembling the toys in a day. The profit is ₹50 each on a toy of type A and ₹60 each on a toy of type B. How many toys of each type would the company manufacture in a day to maximize the profit? Use linear programming to find the solution.
Solution:
Let number of toys of type A and B produced are x and y respectively to maximise the profit. Since, profits on each unit of toys A and B ₹ 50 and ₹ 60 respectively, so, profits on x units of toys A and y units of toy B are ₹ 50x and ₹ 60y respectively. Let Z be total profit.
Then Z = 50x + 60y
Since each unit of toy A and toy B require 5 min and 8 min for cutting. So x units of toy A and y units of toy B require 5x and 8y min, respectively but given maximum time available for cutting 3 × 60 = 180 min. so (first constraint) is given by 5x + 8y ≤ 180
Since each unit of toy A and toy B require 10 min and 8 min for assembling. So, x units of toy A and y units of toy B require 10x and 8y for assembling respectively but given maximum time available for assembling is 4 × 60 = 240 min, so (Second constraint) is given by
10x + 8y ≤ 240
i.e. 5x + 4y ≤ 120
Hence the mathematical formulation of LPP is given below :
maximize Z = 50x + 60y
Subject to constraints,
5x + 8y ≤ 180
5x + 4y ≤ 120
x, y ≥ 0 [Since production can not be less than zero]
Region 5x + 8y ≤ 180 : The line 5x + 8y = 180 meets coordinate axes at A₁(36,0) and B₁\(\left(0, \frac{45}{2}\right)\) respectively.
Region containing origin represents the solution set of 5x + 8y ≤ 180 as (0,0) satisfies 5x + 8y ≤ 180.

Region 5x + 4y ≤ 120 : The line 5x + 4y = 120 meets coordinate axes at C₁(24,0) and D₁(0, 30) respectively.
Region containing origin represents the solution set of 5x + 4y ≤ 120, as (0,0) satisfies Region x, y ≥ 0 : it represent first quadrant of xy plane.
The shaded region OC₁E₁B₁ represents feasible region.
The point E₁(12, 15) is the point of intersection obtained by solving
5x + 8y = 180 and 5x + 4y = 120 simultaneously.

Clearly maximum Z = 1500 at x = 12, y = 15
Thus required Number of toys A = 12, required no. of toys B = 15
and Maximum profit = ₹ 1500

Question 8.
A dietician wishes to mix two kinds of food X and Tin such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:

Food	Vitamin A	Vitamin B	Vitamin C
X	1 unit	2 units	3 units
Y	2 units	2 units	1 unit

One kg of food X costs Rs. 24 and one kg of food F cost Rs. 36. Using Linear Programming, find the least cost of the total mixture which will contain the required vitamins.
Solution:
Let x be the required amount of food X and y be the required amount of food Y that is to be mixed which will produce the required diet. We want to minimise the cost of the diet.
Then the mathematical modelling of the LPP is given as follows :
Minimize Z = 24x + 36y
Subject to constraints;
x + 2y ≥ 10,
2x + 2y ≥ 12
3x + y ≥ 8
and x ≥ 0, y ≥ 0
To solve the LPP, we convert inequation into equation and draw all these lines.
x + 2y = 10, …(1)
2x + 2y= 12 …(2)
3x + y – 8 …(3)
x = 0 =y
line (1) meet coordinate axes at A(10, 0) and D₁(0, 5)
line (2) meet coordinate axes at B(6, 0) and E(0, 6),
Also, line (3) meet coordinate axes at C(8/3, 0) and F(0, 8)
line (1) and (2) intersects at H(2, 4). Also line (2) and (3) intersects at G(l, 5).
The feasible region of the LPP is given shaded area and it is unbounded.

The coordinates of the vertices (Comer – points) of shaded feasible region AHGF are as follows: A(10, 0), H(2, 4), G(1, 5) and F(0, 8).
The values of the objective of function at these points are given in the following table:

Point(x1, x2)	Value of objective function Z = 24x + 36y
A(10,0)	Z = 24 × 10 + 36 × 0 = 240
H(2,4)	Z = 24 ×  2 + 36 × 4 = 192(min)
G(1,5)	Z = 24 × 1 + 36 × 5 = 204
F(0,8)	Z = 16 × 0 + 36 × 8 = 288

Clearly smallest value of Z = 192 at x = 2 ; y = 4
Since region is feasible and unbounded. Further the open half plane 24x + 36y < 192 have no common points in feasible region.
So the smallest value is the minimum value
∴ Z_min= 192 at x = 2, y = 4
Thus, 2 kg of food X and 4 kg of food Y will be required to minimize the cost of the diet.
The least cost of the mixture is ₹ 192.

Question 9.
A company manufactures, two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is ₹40 on each unit of product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufacture so as to earn maximum profit? Use linear programming to find the solution.
Solution:
First of all we arrange the given data in tabular form as follows :

Product (in gms)	Nickel (in gms)	Chromium per each unit	Profit
A B	3 1	1 2	₹ 40 ₹ 50
Maximum availability	9	8

Let the company manufacturer x units of product A and y units of product B respectively.
Since it is given that profit is ₹ 40 on each unit of product A and ₹ 50 on each unit of product B. Then total profit earned by company in x units of product A and y units of product B be ₹ (40x + 50y).
Let Z be the total profit of company.
Then Z = 40x + 50y
The nickel constraint is given by 3x + y ≤ 9 and the chromium constraint is given by x + 2y ≤ 8 Thus, the mathematical modeling of given L.P.P is given as under: Max Z = 40x + 50y
Subject to constraints ;
3x + y ≤ 9
x + 2y ≤ 8
x ≥ 0 ; y ≥ 0 [Since no. of units of product A and B can’t be negative]

For region 3x + y ≤ 9 ; The line 3x + y = 9 meets coordinate axes at A (3,0) and B(0,9).
Since (0, 0) satisfies 3x + y ≤ 9.
Thus region containing (0, 0) gives the soln. set of given region.
For region x + 2y ≤ 8 ; The line x + 2y = 8 meets coordinate axes at C(8,0) and D (0,4).
Since (0, 0) satisfies the given region. Thus region containing (0, 0) gives the soln. set of given region.
x, y ≥ 0 represents the first quadrant of XOY plane.
Both lines 3x + y = 9 and x + 2y = 8 intersects at P (2, 3).
Thus the shaded area OAPD represents the bounded feasible region and its comer points are O (0, 0), A (3, 0); P(2, 3) and D (0, 4).
We evaluate Z at these comer points.

Corner points	Z = 40x + 50y
O(0,0)	0
A(3,0)	40 × 3 = 120
P(2,3)	40 × 2 + 50 × 3 = 230
D(0,4)	40 × 0+50 × 4 = 200

∴ Z_max = 230 at x = 2 and y = 3
Thus the company manufactures 2 units of product A and 3 units of product B to earn maximum profit of ₹ 230.