Well-structured S Chand Class 12 Maths Solutions Chapter 28 Linear Programming Ex 28(a) facilitate a deeper understanding of mathematical principles.
S Chand Class 12 ICSE Maths Solutions Chapter 28 Linear Programming Ex 28(a)
Question 1.
A dealer wishes to purchase a number of geysers and fans. He has only ₹57,600 to invest and has space for at most 20 items. A geyser costs him ₹3600 and a fan ₹2400. His expectation is that he can sell a geyser at a profit of ₹220 and a fan at a profit of ₹180. Assuming that he can sell all the items he can buy, formulate it as a LPP to maximize his profit?
Solution:
Let x be the no. of geysers and y be no. of fans respectively. Since profit on one geyser be ₹220 and on one fan be ₹180 respectively.
Thus profit on x geysers be ₹220 x and on y fans be ₹180y.
Thus total profit of dealer = 220x + 180y
Let Z denote the total profit ∴ Z = 220x + 180y and our objective to maximise the profit Z.
Since he has a space for atmost 20 items.
∴ Corresponding constraint he x +y ≤ 20
Also cost of 1 geyser and 1 fan be ₹3600 and ₹2400 respectively. Then cost of x geysers and y fans be ₹3600x and ₹2400y respectively and he has only ₹57600 to invest.
Thus corresponding constraint is 3600x + 2400y ≤ 57600 ⇒ 3x + 2y ≤ 48
Since fans and geysers cannot be negative ∴ x, y ≥ 0
Hence, the mathematical modelling of given L.P.P is given as under :
Max Z = 220x + 180y
Subject to constraints :
x + y ≤ 20
3x + 2y ≤ 48
x ≥ 0 ; y ≥ 0
Question 2.
A decorative item dealer deals in only two items; wall hangings and artificial plants. He has ₹15000 to invest and a space to store at the most 80 pieces. A wall hanging costs him ₹300 and artificial plant ₹156. He can sell a wall hanging at a profit of ₹50 and artificial plant at a profit of ₹18. Assuming he can sell all the items that he buys, formulate a linear programming problem in order to maximize his profit.
Solution:
Let x be the no. of wall hangings and y be the number of artificial plants. Since it is given that profit on one wall hanging and one artificial plants be ₹50 and ₹18 respectively. Thus, profit on x wall hangings be ₹50x and profit on y artificial plants be ₹18y.
Thus total profit of dealer be ₹50x + 18y and let Z be the total profit. Then Z = 50x + 18y and our objective to maximise the profit Z.
Since it is given that he has a space to store 80 prices. ∴ x + y ≤ 80. Also it is given that cost of one wall hanging and one artificial plant be ₹300 and ₹150. Thus the cost of x wall hangings be 300x and y artificial plants be 150y and he has ₹15000 to invest.
∴ 300x + 150y ≤ 15000 ⇒ 2x + y ≤ 100
Since wall hangings and artificial plant cannot be negative. ∴ x ≥ 0 ; y ≥ 0
Thus the mathematical modeling of given L.P.P is as under : Max Z = 50x + 18y
Subject to constraints ; x + y ≤ 80
2x + y ≤ 100 and x ≥ 0; y ≤ 0
Question 3.
Sarheer wants to invest at most ₹15,000 in Saving certificates and in National Savings Bonds. According to rules, he has to invest at least ₹2000 in Saving certificates and at least ₹3,000 in National Saving Bonds. If the rate of interest on Saving certificates is 8% p.a. and the rate of interest on the National Saving Bonds is 10% p.a.; how should he invest to earn maximum profit. Formulate a LP problem.
Solution:
Let ₹ x be the amount invested in saving certificates and ₹ y be the amount invested in National Saving Bonds.
Total profit = 8% of x + 10% of y = \(\frac { 8 }{ 100 }\)x + \(\frac { 10 }{ 100 }\)y
Let Z be the total profit ∴ Z = \(\frac { 8 }{ 100 }\)x + \(\frac { 10 }{ 100 }\)y and our objective is to maximize Z.
Since he has to invest atleast ₹2000 in Saving certificates.
∴ Corresponding constraint is x ≥ 2000 and he has to invest atleast ₹3000 in bonds.
∴ y ≥ 3000
Also Sameer has to invest atmost ₹15000
∴ Corresponding constraint is x + y ≤ 15000
Thus the mathematical modelling of L.P.P is given as under : Max Z = \(\frac { 8 }{ 100 }\)x + \(\frac { 10 }{ 100 }\)y
Subject to constraints ; x ≥ 2000 ; y ≥ 3000
x + y ≤ 15000
![]()
Question 4.
A retired person wants to invest an amount up to ₹20,000. His broker recommends investing in two types of bonds A and B; bond A yielding 10% return on the amount invested and bond B yielding 15% return on the amount invested. After some consideration, he decides to invest at least ₹5,000 in bond A and at least ₹8000 in bond B. He also wants to invest at least as much in bond A as in bond B. What should his broker suggest if he wants to maximize his return on investments. Formulate LPP.
Solution:
Let ₹ x be the amount invested in bond A and ₹ y be the amount invested in bond B.
∴ Total return on bonds A and B = \(\frac { 10 }{ 100 }\)x + \(\frac { 15 }{ 100 }\)y
Let Z be the total return by retired man
∴ Z = \(\frac { 10 }{ 100 }\)x + \(\frac { 15 }{ 100 }\)y and our aim is to maximise the return.
Since the person has to invest an amount upto ₹ 20000
∴ x + y ≤ 20000
Since the man decides to invest atleast ₹ 5000 in bond A and ₹ 8000 in bond B.
Then corresponding constraints are ; x ≥ 5000 and y ≥ 8000
Thus, the mathematical modelling of given L.P.P is as under : Max Z = \(\frac { 10 }{ 100 }\)x + \(\frac { 15 }{ 100 }\)y
Subject to constraints ; x + y ≤ 20000
x ≥ 5000
y ≥ 8000
x ≥ y
Since he also wants to invest atleast as much in bond A as in bond B.
x ≥ 0 ; y ≥ 0
[since investments in bond A and bond B cannot be negative]
Question 5.
A manufacturer produces TVs and VCR in his factory. Production of each TV requires 4 hours of assembly in workshop 1 and 2 hours of assembly in workshop 2, whereas production of each VCR requires 2 hours of assembly in workshop 1 and 5 hours of assembly in workshop 2. Workshop 1 and workshop 2 function for 40 hours and 60 hours in a week. The profit on each TV is ₹3,000 and each VCR is ₹4,000. Assuming that all TVs and VCR are sold in the market, what should be the strategy of the manufacturer to earn maximum profit Formulate a LP problem.
Solution:
For convenience, we arrange the given data in tabular form as under :
| Workshop No. | TV | VCR | Max no. of hours |
| I | 4 | 2 | 40 |
| II | 2 | 5 | 60 |
Let x be the number of TV and y be the no. of VCR produced by manufacturer.
Since profit on each TV and on each VCR be ₹ 3000 and ₹ 4000 respectively.
∴ Total profit = 3000x + 4000y.
Let Z be the total profit. ∴ Z = 3000x + 4000y and our aim is to maximise Z.
The corresponding constraints are ;
4x + 2y ≤ 40 and 2x + 5y ≤ 60
x ≥ 0 ; y ≥ 0 [no. of TV and VCR’s cant be negative]
Thus, the mathematical modelling of given LPP is given as under :
Max Z = 3000x + 4000y
Subject to constraints ; 4x + 2y ≤ 40 ; 2x + 5y ≤ 60 ; x ≥ 0 ; y ≥ 0
Question 6.
A small scale industrialist produces three types of machines components M1, M2 and M3 made of steel and brass. The amounts of steel and brass required for each component and the number of man-weeks of labour required to manufacture and assemble one unit of each component are as follows.
| M1 | M2 | M3 | Availability | |
| Steel | 6 | 5 | 3 | 100 kg |
| Brass | 3 | 4 | 9 | 75 kg |
| Man-weeks | 1 | 2 | 1 | 20 weeks |
The labour is restricted to 20 man-weeks, steel is restricted to 100 kg per week and the brass to 75 kg per week. The industrialist’s profit on each unit of M1, M2 and M3 is ₹6, ₹4 and ₹7 respectively. Give its mathematical formulation as a linear programming problem such that the total profit is maximum.
Solution:
Let x1, x2 and x3 be the number of machine components M1, M2 and M3 respectively produced by the Industry.
Also it is given that profit on each unit of M1, M2 and M3 be ₹6, ₹4 and ₹7 respectively.
Let Z be the total profit of industry.
∴ Z = 6x1 + 4x2 + 7x3 and our aim is to maximise Z
and corresponding constraints in given problem using data table is as under :
6x1 + 5x2 + 3x3 ≤ 100
3x1 + 4x2 + 9x3 ≤ 75
X1 + 2x2 + x3 ≤ 20
Thus the mathematical modelling of given LPP be as under : max Z = 6x1 + 4x2 + 7x3
Subject to constraints ;
6x1 + 5x2 + 3x3 ≤ 100
3x1 + 4x2 + 9x3 ≤ 75
x1 + 2x2 + x3 ≤ 20
and x1 ≥ 0 ; x2 ≥ 0 ; x3 > 0
[since no. of machine component can’t be negative]
Question 7.
A.cold drink company has three bottling plants, located at two different places. Each plant produces three different drinks A, B and C. The capacities of three plants, in number of bottles per day are as follows.
| Product A | Product B | Product C | |
| Plant I | 3000 | 1000 | 2000 |
| Plant II | 1000 | 1000 | 4000 |
| Plant III | 2000 | 500 | 3000 |
A market survey indicates that during any particular month there will be a demand of 24,000 bottles of A; 16,000 bottles of B and 48,000 bottles of C. The operating costs, per day, of running plants I, II and III are respectively ₹600, ₹400 and ₹500. Formulate it as a linear programming problem to find the number of days. Should the company run each plant during the month so that the production cost is minimized while still meeting up the market demand? Formulate a LP problem.
Solution:
Let the required number of days of running plants I, II and III respectively be x1, x2 and x3.
Also, it is given that operating costs per day of running plants I, II and III are respectively ₹ 600, ₹ 400 and ₹ 500 and let Z be the total production cost.
∴ Z = 600x1 + 400x2 + 500x3 and our aim is to minimised the cost.
Since it is given that, during any particular month there will be a demand of 24000 bottles of A; 16000 bottles of B and 48000 bottles of C.
Then corresponding constraints are :
3000x1 + 1000x2 + 2000x3 ≥ 24000
1000x1 + 1000x2 + 500x3 ≥ 16000
2000x1 + 4000x2 + 3000x3 ≥ 48000
Thus the mathematical modelling of given L.P.P is as under :
Min Z 600x1 + 400x2 + 500x3
Subject to constraints ;
3x1 + x2 + 2x3 > 24
2x1 + 2x2 + x3 ≥ 32
2x1 + 4x2 + 3x3 ≥ 48
x1 ≥ 0 ; x2 ≥ 0 ; x3 ≥ 0
[since the no. of days cannot be negative]
![]()
Question 8.
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F, costs ₹4 per unit and F2 costs ₹5 per unit. A unit of food F, contains at least 3 units of vitamin A and 4 units of minerals. A unit of food F2 contains at least 6 units of vitamin and 3 units of minerals. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements. Formulate this as a linear programming problem.
Solution:
First of all, we arrange the given data in tabular form is given as under :
| Food | Vitamin A | Minerals | Cost per unit |
| F1 F2 |
3 6 |
4 3 |
4 5 |
| Minimum requirement | 80 | 100 |
Let the diet contains x units of food F1 and y units of food F2.
Since it is given that, one unit of food F1 costs ₹ 4 and one unit of food F2 cost ₹5.
Thus the total cost of x units of food F1 and y units of food F2 be ₹(4x – 5y).
Let Z be the total cost ∴ Z = 4x + 5y and our aim is to minimise Z.
Since each unit of F1 contains 3 units of vitamin A and each unit of F2 contains 6 units of vitamin A.
Thus x units of F1 and y units of F2 contains 3x and 6y units of vitamin A.
But the minimum requirement of vitamin A be 80 units.
∴ 3x + 6y ≥ 80.
Similarly x units of F1 and y units of F2 contains 4x units and 3y units of minerals.
But the minimum requirement of minerals be 100 units.
∴ 4x + 3y ≥ 100
Thus the mathematical modelling of given L.P.P is as under :
Min Z = 4x + 5y
Subject to constraints : 3x + 6y ≥ 80 ; 4x + 3y ≥ 10
x ≥ 0 ; y ≥ 0 [since no. of units of Food F1 and F2 can’t be negative]
Question 9.
Vitamins A and B are found in foods F1 and F2. One unit of food F1 contains 20 units of vitamin A and 30 units of vitamin B. One unit of food F2 contains 60 units of vitamin A and 40 units of vitamin B. 1 unit of each of foods F1 and F2 cost ? 3 and ? 4 respectively. The minimum daily requirement (for a person) of vitamins A and B is 80 units and 100 units respectively. Assuming that anything in excess of daily minimum requirements of vitamin A and B is not harmful, find out the optimum mixture of foods F1 and F2 at the minimum cost which meets the daily minimum requirements of vitamins A and B. Formulate the above problem as a LP problem.
Solution:
First of all, we arrange the given data in tabular form is as under :
| Food | Vitamin A | Vitamin B | Cost per unit |
| F1 F2 |
20 60 |
30 40 |
₹ 3 ₹ 4 |
| Minimum requirement | 80 | 100 |
Let the diet contains x units of food F1 and y units of food F2.
Since it is given that one unit of food F1 costs ₹3 and one unit of food F2 costs ₹ 4.
∴ The total cost of x units of food F1 and y units of food F3 = ₹ (3x + 4y)
Let Z be the total cost. ∴ Z = 3x + 4y and we want to minimise Z.
Since one unit of food F1 and F2 contains 20 unit and 60 units of vitamin A respectively. So Total units of vitamin A in x units of Food F1 and y units of food F2 be 20x + 60y.
Also the minimum requirement of vitamin A be 80 units. ∴ 20x + 60y ≥ 80
Also, one unit of Food F1 and F2 contains 30 units and 40 units of vitamin B respectively.
So total units of vitamins B in x units of Food F1 and y units of food F2 be 30x + 40y
But the minimum requirement of vitamin B be 100 units. ∴ 30x + 40y ≥ 100
Thus the mathematical modelling of given L.P.P is as under : Min Z = 3x + 4y
Subject to constraints ; 20x + 60y ≥ 80 ; 30x + 40y ≥100 ; x ≥ 0 ; y ≥ 0
[since no. of units of food F1 and F2 cannot be negative]
Question 10.
A housewife wishes to mix two types of food F1 and F2 in such a way that the vitamins contents of mixture contain at least 8 units of vitamin A and 11 units of vitamin B, food F1 costs ₹60/kg and food F2 costs ₹80/kg. Food F, contains 3 units/kg of vitamin A and 5 units/kg of vitamin B while food F2 contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. For-mulate the above problem as a linear programming problem to minimize the cost of mixture.
Solution:
First of all, we arrange the given data in tabular form is as under :
| Food | Vitamin A | Vitamin B | Cost per unit |
| F1 F2 |
20 60 |
30 40 |
₹ 3 ₹ 4 |
| Minimum requirement | 80 | 100 |
Let the diet contains x units of food F1 and y units of food F2.
Since it is given that one unit of food F1 costs ₹3 and one unit of food F2 costs ₹4.
∴ The total cost of x units of food F1 and y units of food F3 = ₹ (3x + Ay)
Let Z be the total cost. ∴ Z = 3x + Ay and we want to minimise Z.
Since one unit of food F1 and F2 contains 20 unit and 60 units of vitamin A respectively. So Total units of vitamin A in x units of Food F1 and y units of food F2 be 20x + 60y.
Also the minimum requirement of vitamin A be 80 units. ∴ 20x + 60y ≥ 80
Also, one unit of Food F1 and F2 contains 30 units and 40 units of vitamin B respectively.
So total units of vitamins B in x units of Food F1 and y units of food F2 be 30x + 40y
But the minimum requirement of vitamin B be 100 units. ∴ 30x + 40y ≥ 100
Thus the mathematical modelling of given L.P.P is as under : Min Z = 3x + 4y
Subject to constraints ; 20x + 60y ≥ 80 ; 30x + 40y ≥ 100; x ≥ 0; y ≥ 0
[since no. of units of food F1 and F2 cannot be negative]
Question 11.
A small manufacturing firm produces two types of gadgets, A and B which are first processed in the foundry, then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for the production of each unit of A and of B and the number of man-hours the firm has available per week are as under:
| Foundry | Machine shop | |
| Garget A | 10 | 5 |
| Garget B | 6 | 4 |
| Firm’s capacity per week | 1000 | 600 |
The profit on the sale of A is ₹30 per unit as compared with ₹20 per unit of B.
The problem is to determine the weekly, production of gadgets A and B, so that total profit is maximized.
formulate the above problem as a linear programming problem.
Solution:
The given data in tabular form is given as under :
| Gadget | Foundry | Machine shop | Profit |
| A B |
10 6 |
5 4 |
₹ 30 ₹ 20 |
| Firm’s capacity per week | 1000 | 600 |
Let the required weekly production of gadgets A and B be x and y respectively.
Given that, profit on sale on each gadget A is ₹ 30
So, profit on x gadgets of type A = 30x
Profit on sale on each gadget of type B = ₹ 20
So, profit on y gadgets of type B = 20y
Let Z denote the total profit. Then Z = 30x + 20y
Given, production of one unit of gadget A requires 10 hours per week for foundry and one unit of gadget B requires 6 hours per week for foundry.
So, x units of gadget A requires 10x hours per week and y units of gadget B requires by hours per week. But given the maximum capacity of foundry per week is 1000 hours, Thus, the first constraint is given by 10x + 6y ≤ 1000
Given, production of one unit of gadget A requires 5 hours per week of machine shop and production of one unit of gadget B requires 4 hours per week of machine shop.
So, x units of gadget A requires 5x hours per week and y units of gadget B requires 4y hours per week, but given the maximum capacity of machine shop is 600 hours per week. Thus the second constraint be
5x + 4y ≤ 600
Hence, the mathematical formulation of LPP is as follows :
Maximize Z = 30x + 20y
Subject to constraints,
10x + 6y ≤ 1000
5x + 4y ≤ 600
and, x, y ≥ 0 [Since production cannot be less than zero i.e. negative]
Question 12.
A certain manufacturer has 75 kg of cashew and 120 kg of groundnuts. These are to be mixed in 1 kg packages as follows; a low grade mixture 250 g of cashew, 750 g of groundnuts, whereas in a high grade mixture 500 g of cashew and 500 g of groundnuts. If the profit on low grade mixture is ₹2 per package and that of high grade mixture is ₹3 per package, how many packages of each mixture be made for a maximum profit? For this problem, derive the inequations and write the objective function. You need not draw the graph.
Solution:
First of all, we arrange the given data in tabular form is as under :
| Mixture | Cashew | Groundnuts | Profit |
| Low grade mixture High grade mixture |
250 g 500 g |
750 g 500 g |
₹ 2 ₹ 3 |
| Maximum availability | 75 kg | 120 kg |
Let x be the no. of packages of Low grade mixture and y be the no. of packages of high grade mixture.
Since it is given that profit on each package of low grade and high grade mixture be ₹ 2 and ₹ 3 respectively. Thus total profit on x packages of low grade mixture and y packages of high grade mixture be ₹(2x + 3y) and let Z be the total profit. ∴ Z = 2x + 3y and our aim is to maximise the profit.
Further total cashew constraint is given by 250x + 500y ≤ 75000 i.e. x + 2y ≤ 300
and Total groundnut constraint is given by 750x + 500y ≤ 120000 ⇒ 3x + 2y ≤ 480
Thus the mathematical modelling of given L.P.P is given as under : Max Z = 2x + 3y
Subject to constraints ;
x + 2y ≤ 300
3x + 2y ≤ 480
x ≥ 0 ; y ≥ 0 [since no. of packages can’t be negative]
Question 13.
A manufacturer has three machines I, II and III installed in his factory. Machines I and II are capable of being operated for at the most 12 hours, whereas machine III must be operated at least for 5 hours a day. He produces only two items, each requiring the use of the three machines. The number of hours required for producing 1 unit of each of the items A and B on the three machines are given in the following table:
| Items | Number of hours required on the machines | ||
| I | II | III | |
| A | 1 | 2 | 1 |
| B | 2 | 1 | 5/4 |
He makes a profit of ₹60 on item A and ₹40 on item B. Assuming that he can sell all that he produces, how many of each item should he produce so as to maximize his profit? Formulate the above problem as a linear programming problem.
Solution:
Let the number of items A and B are required.be x and y to maximize profit.
Given profits on one item A and B are ₹6 and ₹4 respectively So, profit on x items of type A and y items of type B are ₹ 6x and ₹ 4y respectively.
Let the total profit be Z, then Z = 6x + Ay
Given, machine I works 1 hour and 2 hours on item A and B respectively, so, x number of item A and y number of item B need x hour and 2y hours on machine I respecti vely, but given machine I works at most 12. hours, so (first constraint) is given by x + 2y ≤ 12
Given, machine II works 2 hours and 1 hours on item A and B respectively, so,
x number of item A and y number of item B need 2x hours and y hour on machine II, but given machine II works maximum 12 hours, so (second constraint) is given by 2x + y ≤ 12
Given, machine III works 1 hours and \(\frac { 5 }{ 4 }\) hour on one item A and B respectively, Then
x number of item A and y number of item B needs x hours and \(\frac { 5 }{ 4 }\)y hours respectively on machine
III, but given machine III works at least 5 hours, then (third constraint) is given by
x + \(\frac { 5 }{ 4 }\) y ≥ 5
4x + 5y ≥ 20
Hence the required mathmatical formulation of LPP, is given below :
max Z = 6x + 4y
x + 2y ≤ 12
2x + y ≤ 12
4x + 5y ≤ 20
x,y ≥ 0 [since number of item A and B not be less than zero]
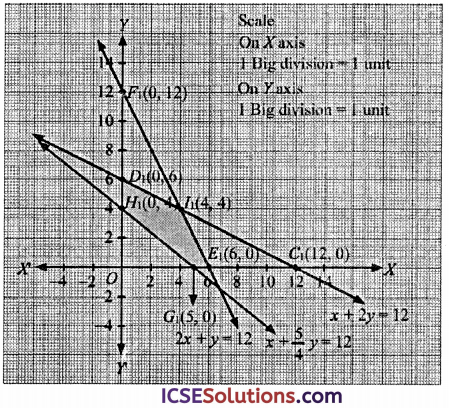
Region x + 2y ≤ 12 : line x + 2y = 12 meets axes at C1(12, 0) and D1(0,6) respectively. Region containing origin represents the solution set of x + 2y ≤ 12 as (0,0) satisfies x + 2y ≤ 12.
Region 2x + y ≤ 12; The line 2x + y = 12 meets coordinate axes at E1(6,0) and F1(0,12). So region containing (0,0) represents the solution set of 2x +y ≤ 12 since (0,0) satisfies 2x+y ≤ 12. line (1) and line (2) intersects at I1(4,4).
Region Ax + 5y ≥ 20: line 4x + 5y = 20 meets coordinate axes at G1(5,0) and H1(0,4) respectively, Region not containing origin represents the solution set of Ax + 5y ≥ 20 as (0,0) does not satisfy Ax + 5y ≥ 20.
Region x, y ≥ 0: it represent the first quadrant.
Shaded region E1G1H1D1I1 represents the feasible region.
| Corner point | Z = 6x + 4y |
| E1 (6, 0) | 6 (6) + 4 (0) = 36 |
| G1 (5, 0) | 6 (5) + 4 (0) = 30 |
| H1 (0, 4) | 6 (0) + 4 (4) = 16 |
| D1 (0, 6) | 6 (0) + 4 (6) = 24 |
| I1 (4, 4) | 6 (4) + 4 (4) = 40 |
Hence, Z is maximum at x = 4, y = 4 and Zmax = 40
Required number of product A = 4, product B = 4 & Miximum profit = ₹40.
![]()
Question 14.
A company makes three different products A, B and C by combining steel and rubber. Products requires 2 units of steel and 3 units of rubber and can be sold at a profit of ₹ 40 per unit. Product B requires 3 units of steel and 3 units of rubber and can be sold at a profit of ₹ 45 per unit. Product C requires 1 unit of steel and 2 units of rubber and can be sold at a profit of ₹ 24 per unit. There are 100 units of steel and 120 units of rubber available per day. What should be daily production of each of the products, so that the combined profit is maximum?
Solution:
First of all, we arrange the given data in tabular form is as under :
| Products | Steel | Rubber | Profit per unit |
| A B C |
2 3 1 |
3 3 2 |
₹ 40 ₹ 45 ₹ 24 |
| Maximum availability | 100 | 120 |
Let the company produces x, units of product A, x2 units of product B and x3 units of product C. From table, steel constraints is given by 2x1 + 3x2 + x3 ≤ 100
and rubber constraint is given by 3x1 + 3x2 + 2x3 ≤ 120
Since it is given that, profit on one unit of product A, B and C be ₹ 40, ₹ 45 and ₹ 24 respectively.
Thus total profit gained by company on selling x1 units of product A, x2 units of product B and x3 units of product C be ₹(40x1 + 45x2 + 24x3) and let Z be the total profit of company.
Then Z = 40x1 + 45x2 + 24x3 and our aim to maximise Z.
Thus the mathematical modelling of given L.P.P is as under :
Max Z = 40x1 + 45x2 + 24x3
Subject to constraints ; 2x1 + 3x2 + x3 ≤ 100
3x1 + 3x2 + 2x3 ≤ 120
and x1 ≥ 0 ; x2 ≥ 0 ; x3 ≥ 0
[since no. of units of product A, B and C cannot be negative]
Question 15.
There is a factory located at each of the two places P and From these locations a certain commodity is delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are, respectively, 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are, respectively, 8 and 6 units. The cost of transportation per unit is given below:
| From | To | Cost (₹/unit) | ||
| P C |
A | B | C | |
| 16
10 |
10
12 |
15
10 |
||
How many units should be transported from each factory to each depot in order that the transportation cost is minimum? Formulate the above linear programming problem mathematically.
Solution:
Let the number of commodity supplied by place P to depot A and B be x units and y units respectively. Thus the no. of commodity supplied by place P to depot C be (8 – x – y) units.
The weekly requirement of depot A be 5 units of commodity. Out of which x units of commodity is supplied by place P so remaining (5 – x) units of commodity is supplied by place Q. Similarly the supply of commodity from place Q to depot B be (5 – y) units and to depot C be (x + y – 4) units.
The above information is shown in figure alongside. The transportation cost (in ₹) from two places P and Q to three depots A, B and C are ;

depot A : 16x + (5 – x) 10 = 50 + 6x
depot B : 10y + 12 (5 – y) = 60 – 2y
depot C : 15 (8 – x – y) + 10 (x + y – 4) = – 5x – 5y + 80
∴ Total transportation cost from places P and Q to all three depots A, B and C
= ₹ [50 + 6x + 60 – 2y – 5x – 5y + 180]
= ₹ [190 + x – 7y]
Let Z be the total transportation cost
∴ Z = 190 + x – 7y
and our aim is to minimise the cost and constraints are ; commodity can’t be negative
∴ 8 – x – y ≥ 0 ⇒ x + y ≤ 8 and 5 – x ≥ 0; 5 – y ≥ 0; x + y – 4 ≥ 0
Thus, the mathematical modelling of given L.P.P is given as under :
Min Z = 190 + x – 7y
Subject to constraints ; x + y ≤ 8 ; x ≤ 5 ; y ≤ 5 ; x + y ≥ 4 ; x ≥ 0 ; y ≥ 0 [since no. of units of commodities can’t be negative]