ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 13 Understanding Quadrilaterals Objective Type Questions
Mental Maths
Question 1.
Fill in the blanks:
(i) The curves which have different beginning and end points are called …………
(ii) A curve which does not cross itself at any point is called a …………
(iii) A simple closed curve made up entirely of line segments is called a …………
(iv) A polygon in which each interior angle is less than 180° is called a …………
(v) 10 sided polygon is called …..
(vi) A polygon which has all its sides of equal length and all its angles of equal measure is called a …………
(vii) Sum of all exterior angles of a polygon is …………
(vi) A polygon which has all its sides of equal length and all its angles of equal measure is called a …………
(vii) Sum of all exterior angles of a polygon is …………
(viii) Sum of all interior angles of a n-sided polygon is …………
(ix) The adjacent angles of a parallelogram are …………
(x) If an angle of a parallelogram is a right angle, then it is called a …………
(xi) If two adjacent sides of a parallelogram are equal, then it is called a …………
(xii) It two adjacent sides of a rectangle are equal, then it is called a …………
(xiii) The diagonal of a rhombus bisect each other at …………
(xiv) A quadrilateral in which one pair of opposite sides is parallel is called a …………
(xv) A quadrilateral in which two pairs of adjacent sides are equal is called a …………
(xvi) If two non-parallel sides of a trapezium are equal then it is called …………
Solution:
(i) The curves which have different beginning
and end points are called open curves.
(ii) A curve which does not cross itself
at any point is called a simple curve.
(iii) A simple closed curve made up entirely
of line segments is called a polygon.
(iv) A polygon in which each interior angle
is less than 180° is called a convex polygon.
(v) 10 sided polygon is called decagon.
(vi) A polygon which has all its sides of equal length
and all its angles of equal measure is called a regular polygon.
(vii) Sum of all exterior angles of a polygon is 360°.
(viii) Sum of all interior angles of a n-sided polygon is
(n – 2) × 180° or (2n – 4) × 90°.
(ix) The adjacent angles of a parallelogram are supplementary.
(x) If an angle of a parallelogram is a right angle,
then it is called a rectangle.
(xi) If two adjacent sides of a parallelogram are equal,
then it is called a rhombus.
(xii) It two adjacent sides of a rectangle are equal,
then it is called a square.
(xiii) The diagonal of a rhombus bisect each other at right angles.
(xiv) A quadrilateral in which one pair of
opposite sides is parallel is called a trapezium.
(xv) A quadrilateral in which two pairs of
adjacent sides are equal is called a kite.
(xvi) If two non-parallel sides of a trapezium
are equal then it is called an isosceles trapezium.
Question 2.
State whether the following statements are true (T) or false (F):
(i) The curves which have same beginning and end points are called open curves.
(ii) The region of the plane that lies inside the curve is called interior of curve.
(iii) A polygon in which atleast one interior angle is greater than 180° is called convex polygon.
(iv) 6 sided polygon is called hexagon.
(v) Sum of all interior angles of a quadrilateral is 180°.
(vi) Each interior angle of a n-sided regular polygon is \(\frac{(2 n-4) \times 90^{\circ}}{n}\).
(vii) The diagonals of a parallelogram bisect each other at right angles.
(viii) The opposite angles of a parallelogram are of equal measure.
(ix) The diagonals of a rhombus bisect the angles of rhombus.
(x) The diagonals of a square are not equal.
(xi) Co-interior angles of a parallelogram are supplementary.
(xii) The diagonals of a kite bisect at right angles.
(xiii) All rectangles are squares.
(xiv) All rhombuses are parallelograms.
(xv) All squares are rhombuses and also rectangles.
(xvi) All squares are not parallelograms.
(xvii) All kites are rhombuses.
(xviii) All rhombuses are kites.
(xix) All parallelograms are trapeziums.
(xx) All squares are trapeziums.
Solution:
(i) The curves which have same beginning
and end points are called open curves. False
Correct:
It is called a closed curve.
(ii) The region of the plane that lies inside
the curve is called interior of curve. True
(iii) A polygon in which atleast one interior angle is
greater than 180° is called convex polygon. False
Correct:
It is called a concave polygon.
(iv) 6 sided polygon is called hexagon. True
(v) Sum of all interior angles of a quadrilateral is 180°. False
Correct:
The sum is 360°.
(vi) Each interior angle of a n-sided regular polygon is \(\frac{(2 n-4) \times 90^{\circ}}{n}\). True
(vii) The diagonals of a parallelogram bisect each other at right angles. False
(viii)The opposite angles of a parallelogram are of equal measure. True
(ix) The diagonals of a rhombus bisect the angles of rhombus. True
(x) The diagonals of a square are not equal.
False
Correct:
Diagonals are equal.
(xi) Co-interior angles of a parallelogram are supplementary. True
(xii) The diagonals of a kite bisect at right angles. False
(xiii) All rectangles are squares. False
Correct:
Some rectangle whose sides are equal are squares.
(xiv) All rhombuses are parallelograms. True
(xv) All squares are rhombuses and also rectangles. True
(xvi) All squares are not parallelograms. False
Correct:
All squares are parallelograms.
(xvii) All kites are rhombuses. False
Correct : A kite with all sides equal is a rhombus.
(xviii) All rhombuses are kites. True
(xix) All parallelograms are trapeziums. True
(xx) All squares are trapeziums. True
Multiple Choice Questions
Choose the correct answer from the given four options (3 to 19):
Question 3.
Sum of all interior angles of a 11-sided polygon is
(a) 1620°
(b) 1440°
(c) 1260v
(d) none of these
Solution:
Sum of all interior angles of an 11-sided polygon is
= (2 × n – 4 ) × 90°
= (2 × 11 – 4) × 90°
= 18 × 90 = 1620 (a)
Question 4.
If each interior angle of a regular polygon is 144°, then number of sides of polygon is
(a) 8
(b) 9
(c) 10
(d) 11
Solution:
Each interior angle of a regular polygon is 144°
Then \(\frac{2 n-4}{n}\) × 90° = 144°
⇒ \(\frac{2 n-4}{n}=\frac{144^{\circ}}{90^{\circ}}\)
⇒ 10n – 20° = 8n
⇒ 10n – 8n = 20°
⇒ 2n = 20°
⇒ n = 10
∴ It is 10-sided polygon. (c)
Question 5.
If the sum of all interior angles of a polygon is 1260°, then number of sides of polygon is
(a) 6
(b) 7
(c) 8
(d) 9
Solution:
Sum of all interior angles of a polygon = 1260°
∴ (2n – 4) × 90° = 1260°
⇒ 2n – 4 = \(\frac{1260^{\circ}}{90}\)
⇒ 2n = 14 + 4 = 18
⇒ n = \(\frac{18}{2}\) = 9
∴ Polygon is 9-sided. (d)
Question 6.
The sum of all exterior angles of a pentagon is
(a) 590°
(b) 360°
(c) 180°
(d) none of these
Solution:
Sum of exterior angles of a pentagon = 360° (b)
Question 7.
If the ratio between an exterior and interior angle of a regular polygon is 1 : 5, then the number of sides of the polygon is
(a) 11
(b) 12
(c) 13
(d) 14
Solution:
Ratio between exterior angle and interior angle
of a regular polygon = 1 : 5
But sum of angles = 180°
∴ Exterior angle = \(\frac{180^{\circ}}{1+5}\) × 1
= \(\frac{180^{\circ}}{6}\) = 30°
∴ Number of sides = \(\frac{360^{\circ}}{30}\) =12 (b)
(Sum of exterior angles = 360°)
Question 8.
In the given figure, the value of x is
(a) 140°
(b) 50°
(c) 130°
(d) 40°

Solution:
In the given figure,
Sum of exterior angles of a triangle = 360°
∴ 140° + x + 90° = 360°
⇒ x + 230° = 360°
∴ x = 360° – 230° = 130° (c)
Question 9.
In the given figure, the value of x is
(a) 120°
(b) 130°
(c) 140°
(d) 150°

Solution:
In the given figure,
Sum of angles of a quadrilateral = 360°
∴ 60° + (180° – 120°) + 110° + x = 360°
⇒ 60° + 60° + 110° + x = 360°
230° + x = 360°
∴ x = 360°- 230° = 130° (b)
Question 10.
In the given figure, the value of x + y + z + w is
(a) 180°
(b) 270°
(c) 300°
(d) 360°

Solution:
In the given figure,
Sum of exterior angles of a quadrilateral = 360°
∴ x + y + z + w = 360° (d)
Question 11.
In the given figure, the value of x + y is
(a) 180°
(b) 190°
(c) 170°
(d) 160°

Solution:
In the given figure,
Sum of interior angles of a quadrilateral = 360°
60° + y + 110° + x = 360°
⇒ x + y + 170° = 360°
⇒ x + y = 360° – 170°
x + y = 190° (b)
Question 12.
The lengths of two adjacent sides of a parallelogram are in the ratio 1 : 2. If the perimeter of parallelogram is 60 cm, then length of its sides are
(a) 6 cm, 12 cm
(b) 8 cm, 16 cm
(c) 9 cm, 18 cm
(d) 10 cm, 20 cm
Solution:
Ratio in the length of two adjacent sides of a parallelogram = 1 : 2
Perimeter = 60 cm
∴ Sum of two adjacent sides = \(\frac{60}{2}\) = 30 cm
Let first side = x, then second side = 2x
∴ x + 2x = 30 ⇒ 3x = 30
x = \(\frac{30}{2}\) = 10 cm
First side = 10 cm
and second side = 10 × 2 = 20 cm (d)
Question 13.
In the given figure, ABCD is a parallelogram, the values of x and y respectively are
(a) 1 cm, 1 cm
(b) 2 cm, 1 cm
(c) 1 cm, 2 cm
(d) 2 cm, 2 cm

Solution:
In the given figure, ABCD is a parallelogram
∵ Diagonals of a parallelogram bisect each other
∴ AO = OC and BO = OD
∴ 6 = 5x + 1
⇒ 5x = 6 – 1 = 5
⇒ x = \(\frac{5}{5}\)
and y + 3 = 4
⇒ y = 4 – 3 = 1
∴ x = 1, y = 4 (a)
Question 14.
In the given figure, ABCD is a parallelogram, the values of x, y and z respectively are
(a) 60°, 60°, 70°
(b) 60°, 70°, 60°
(c) 70°, 60°, 60°
(d) none of these

Solution:
In the given figure,

ABCD is a parallelogram, BD is its one diagonal
∠ABD + ∠DBC +∠CBE = 180°
(Angles on one side of a line)
⇒ 50° + x + 70° = 180°
x + 120° = 180°
∴ x = 180° – 120° = 60°
But y = x (Alternate angles)
∴ y = 60°
z = 70° (Alternate angles)
∴ x = 60°, y = 60°, z = 70° (a)
Question 15.
In the given figure, ABCD is a rectangle, the value of angle x is
(a) 60°
(b) 90°
(c) 120°
(d) none of these

Solution:
In the given figure, ABCD is a rectangle

∴ ∠OBA = ∠OAB = 30°
In ∆AOB,
∠AOB = ∠COD (Vertically opposite angles)
∠AOB = x
∠AOB + ∠OBA + ∠OAB = 180° (Angles of a triangle)
⇒ x + 30° + 30° = 180°
⇒ x = 180°- 30°- 30° = 120°
∴ x = 120° (c)
Question 16.
In a rhombus ABCD, the diagonals AC and BD are respectively 8 cm and 6 cm. The length of each side of the rhombus is
(a) 7 cm
(b) 5 cm
(c) 6 cm
(d) 8 cm
Solution:
In rhombus ABCD
Diagonals AC and BD are 8 cm and 6 cm

∴ AC = 8 cm and BD = 6 cm
∵ Diagonals of a rhombus bisect each other at right angles
AO = OC = \(\frac{8}{2}\) = 4 cm,
BO = OD = \(\frac{6}{2}\) = 3 cm
∴ In right ∆AOB
AB = \(\sqrt{\mathrm{AO}^{2}+\mathrm{BO}^{2}}=\sqrt{4^{2}+3^{2}}\)
= \(\sqrt{16+9}=\sqrt{25}\) = 5 cm
Each side of rhombus = 5 cm (b)
Question 17.
In the given figure, ABCD is a square, the value of angle x is
(a) 30°
(b) 45°
(c) 60°
(d) not possible to find
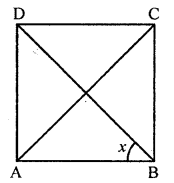
Solution:
In the given figure,
ABCD is a square whose diagonals AC and BD
bisect each other at O.

∵ Diagonals of a square bisect the opposite angles.
∴ x = \(\frac{1}{2}\) × ∠B = \(\frac{1}{2}\) × 90° = 45° (b)
Question 18.
In the given figure, ABCD is a kite, the value of angle x is
(a) 86°
(b) 100°
(c) 104°
(d) none of these

Solution:
In the given figure, ABCD is a kite whose
diagonals AC and BD intersect at O at right angles.

In ∆OAB, ∠O = 90°
∴ ∠OAB + ∠ABO = 90°
⇒ ∠OAB + 36° = 90°
⇒ ∠OAB = 90° – 36° = 54°
But ∠OAD = ∠OCD = 50°
x = ∠DAO + ∠AOB
⇒ x = 50° + 54°= 104° (c)
Question 19.
In the given figure, ABCD is an isosceles trapezium. The values of x, y and z respectively are
(a) 110°, 110°, 70°
(b) 110°, 70°, 110°
(c) 70°, 110°, 110°
(d) none of these

Solution:
In isosceles trapezium ∠A = 70°
But ∠B = ∠A = 70° ⇒ z = 70°
But x + 70° = 180°
⇒ x = 180°-70°= 110°
But y = x = 110°
∴ 110°, 110°, 70° (a)
Higher Order Thinking Skills (Hots)
Question 1.
In the given figure, ABCDEF is a regular hexagon. Prove that quadrialterals ABDE and ACDF are parallelograms. Also prove that quadrilateral AGDH is a parallelogram.

Solution:
In the given figure, ABCDEF is a regular hexagon.
AC, AE, DF, DB are joined.

To prove: ABDE, ACDF and AGDH are ||gm
Proof: In ∆BCD,
BC = CD
∴ ∠CBD = ∠CDB = 30° (∵ ∠C = 120° angle of hexagon)
But ∠B = ∠D (Angles of a regular hexagon)
∴ ∠B – ∠CBD = ∠D – ∠CDB
⇒ ∠ABD = ∠BDE = 90°
Similarly, ∠FAB = ∠AED = 90°
∴ ∠ABD + ∠BDE = 90° + 90° = 180°
But they are cointerior angle.
∴ AB || DE
∴ ABDE is a ||gm
Similarly we can prove that ACDF is a parallelogram.
∵ AC || DF and BD || AC
∴ AGDH is a parallelogram.
Question 2.
In the given figure, ABCD is a parallelogram and M, N are the mid-points of sides BC, AD respectively. Prove that EA = AB = BF.

Solution:
In the given figure,
ABCD is a parallelogram M and N are
midpoints of the sides BC and AD respectively.
To prove : EA = AB = BF.
Proof: In ∆AFD,
M is the midpoint of BC and BC || AD
∴ B is mid-point of AF
∴ AB = BF …(i)
Similarly in ∆EBC,
N is the midpoint of AD and AD || BC
∴ A is the midpoint of EB
∴ EA = AB …(ii)
From (i) and (ii),
EA = AB = BF
Question 3.
Prove that the quadrilateral formed by joining the mid-points of the adjacent sides of a rectangle is a parallelogram.
Solution:
Given : ABCD is a rectangle.
P, Q, R and S are the mid points of the sides
AB, BC, CD and DA respectively.
PQ, QR, RS and SP are joined.
To prove : PQRS is a parallelogram.
Construction : Join AC and BD.

Proof: In ∆ABC,
P and Q are mid points of AB and BC respectively
∴ PQ || AC and PQ = \(\frac{1}{2}\) AC …(i)
Similarly in ∆ADC
SR mid points of AD and CD respectively
∴ SR || AC and SR = \(\frac{1}{2}\) AC …(ii)
From (i) and (ii),
SR || PQ and SR = PQ
∴ PQRS is a parallelogram.