ML Aggarwal Class 12 Maths Solutions Section A Chapter 1 Relations and Functions Ex 1.3

Students often turn to ML Aggarwal Class 12 ISC Solutions Chapter 1 Relations and Functions Ex 1.3 to clarify doubts and improve problem-solving skills.

ML Aggarwal Class 12 Maths Solutions Section A Chapter 1 Relations and Functions Ex 1.3

Question 1.
Let A = {1, 2}, B = {3, 6), function f ∴A → B be defined by f(x) = 3x and function g ∴A → B be defined by g(x) = x² + 2. Show thatf g.
Solution:
Given A = {1, 2) and B = {3, 6)
Given f ∴A → B defined by f(x) = 3x
and g ∴A → B defined by g(x) = x² + 2
Here, D_f = D_g = A
f(1) = 3 × 1 = 3;
g(1) = 1² + 2 = 3
f(2) = 3 × 2 = 6 ;
g (2) = 2² + 2 = 6
∴ f(x) = g (x) ∀ x ∈ D_f = D_g
Hence f = g [using def. of equal functions]

Question 2.
Check the injectivity and surjectivity of the following functions :
(i) f : N → N defined by f(x) = x² (NCERT)
(ii) f : Z → Z defined by f(x) = x² (NCERT)
(iii) f : R → R defined by f(x) = x² (NCERT)
(iv) f  : N → Q defined by f(x) = x³
(v) f : Z → Z defined by f(x) = x³ (NCERT)
(vi) f : R → R defined by f(x) = x³
Solution:
(i) Given f : N → N defined by f(x) = x²
∀ x, y ∈ N s.t. f(x) = f(y)
⇒ x² – y²
⇒ (x – y) (x + y) = 0
⇒ x = y = 0
[x + y ≠ 0 ∀ x, y ∈ N]
⇒ x = y
∴ f is one-one.
Since 2 ∈ N (codomain).
Then x² = 2
⇒ x = ± √2 ∉ N
i.e. 2 has no pre-image in N (domain)
∴ f is not onto.
Thus, f is one-one but not onto.

(ii) Given f : Z → Z defined by f(x) = x² ∀ x ∈ Z since 1, – 1 ∈ Z and
f(1) = 1² = 1 and
f(- 1) = (- 1)² = 1
i.e. different element in Z have same images in Z.
Thus f(- 1) = f(1) = 1
∴ f is many one.
Since negative integers have no pre-images.
∴ f is not onto.
Thus f is neither 1-1 nor onto.

(iii) Given f : R -> R defined by f(x) = x² ∀ x, y ∈ R
s.t f(x) = f(y)
⇒ x² = y²
⇒ x = ±y
⇒ x ≠ y
Thus f is not 1 – 1 i.e. f is not injective.
Also 1, – 1 ∈ R (domain of f) we have f(1) = f(- 1) = 1
i.e. different elements have same images Thus f is not injective.

Subjectivity :
y ∈ R (co domain of f) be any arbitrary element
s.t f(x) = y
⇒ x² = y
⇒ x = ± √y
since y ∈ R
⇒ ± √y ∉ R
⇒ x ∉ R
Thus, ∀ y ∈ R ∉ x ∈ R s.t f(x) = y
f is not onto i.e. subjective.
Since negative real numbers have no pre-images in R.
Thus f is neither injective nor surjective.

(iv) Given f : N → Q defined by
f(x) = x³ ∀ x, y ∈ N s.t f(x) = f(y)
⇒ x³ = y³
⇒ x³ – y³ = 0
⇒ (x – y) (x² + xy + y²) = 0
⇒ x – y = 0 [∵ x² + xy + y² ≠ 0 ∀ x, y ∈ N]
⇒ x = y
Thus f is injective i.e. one-one.

Subjectivity :
Let y ∈ Q be any arbitrary element
Then f(x) = y
⇒ x³ = y
⇒ x = y^1/3
since y ∈ Q
⇒ y^1/3 ∉ N
⇒ x ∉ N
Thus ∀ y ∈ Q ∉ x ∈ N s.t y = f(x)
∴ f is not surjective.

(v) Given f : Z → Z defined by f(x) = x³
∀ x ∈ Z such that f(x) = f(y)
⇒ x³ = y³
⇒ x = y
∴ f is one-one.
Let y ∈ Z be any arbitrary element of Z.
Then f(x) = y
⇒ x³ = y
⇒ x = y^1/3
Since y ∈ Z
⇒ y^1/3 ∉ Z
∴ x ∉ Z
such that f(x) = y.
∴ f is not surjective.

(vi) Given f : R → R defined by f(x) = x³ + 1 ∀ x, y ∈ R
such that f(x) = f(y)
⇒ x³ + 1 = y³ + 1
⇒ (x – y) (x² + xy + y²) = 0
⇒ x³ = y³
⇒ (x – y) (x² + xy + y²) = 0
⇒ x = y
∴ f is one-one.
Let y ∈ R be any arbitrary element.
Then f(x) = y
⇒ x³ + 1 = y
⇒ x = (y – 1)^1/3
since y ∈ R
⇒ (y – 1)^1/3 ∈ R
⇒ x ∈ R
Thus ∀ y ∈ R ∈ x = (y – 1)^1/3 ∈ R
such that
f(x) = f[(y – 1)^1/3] = [(y – 1)^1/3]³ + 1
= y – 1 + 1 = y
∴ f is onto.
Hence f is 1-1 and onto.
∴ f is bijective.

Question 3.
Let I be the set of all integers. Show that the function f : I → I defined by f(x) = | x | is neither one-one nor onto.
Solution:
Given f : R → R defined by f(x) = | x |
Clearly 1, – 1 ∈ R s.t. f(1) = | 1 | = 1 and
f(- 1) = |- 1| = 1
∴ different elements of R (domain) have same image in R (codomain)
∴ f is not one-one.
Clearly negative integers have no pre-image in I (domain)
∴ f is not surjective.
Thus f is neither injective nor surjective.

Question 4.
Show that the function f : R → R defined by f(x) = 3x² – 2 is many-one into.
Solution:
Given f : R → R defined by f(x) = 3x² – 2
∀ x, y ∈ R s.t f(x) = f(y)
⇒ 3x² – 2 = 3y² – 2
⇒ 3x² = 3y²
⇒ x = ±y
⇒ x ≠ y
∴ f is not 1 – 1, thus f is many one.
Further 1, – 1 ∈ R,
f(1) = f(- 1) = 3 – 2 = 1
i.e. different elements have same images
∴ f is many-one.
Lety y ∈ R be any arbitrary element then f(x) = y
⇒ 3x² – 2 = y
⇒ x = ± \(\sqrt{\frac{y+2}{3}}\) ∉ R ∀ y ∈ (- ∞, – 2)
Now – 3 ∈ R then f(x) = – 3
⇒ 3x² – 2 = – 3
⇒ 3x² = – 1
⇒ x² = – \(\frac{1}{3}\)
⇒ x = ± \(\sqrt{-\frac{1}{3}}\) ∉ R
∴ – 3 has no pre-image in R (domain of f)
∴ f is into.
Hence f is many one and into.

Question 5.
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and f : {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one but not onto.
Solution:
Given A = {1, 2, 3} and B = {4, 5, 6, 7} and f be a function from A to B be given by {(1, 4), (2, 5), (3, 6)}
Clearly different elements of A have different images in B .
∴ f is one-one.
Clearly 7 ∈ B and it has no pre-image in A under f.
∴ f is not onto.
Hence f is one-one but not onto.

Question 6.
In each of the following cases, state whether the function is bijective or not. Justify your answer.
(i) f : R → R defined by f(x) = 2x + 1
(ii) f : R → R defined by f(x) = 3 – 4x (NCERT)
(iii) f : R → R defined by f(x) = 1 + x². (NCERT)
Solution:
(i) Given,
f : R → R defined by f(x) = 2x + 1
∀ x, y ∈ R s.t f(x) = f(y)
∈ 2x + 1 = 2y + 1
⇒ 2x = 2y
⇒ x = y
∴ f is one-one.

Surjectivity :
Let y ∈ R be any arbitrary element
Then f(x) = y
⇒ 2x + 1 = y
⇒ x = \(\frac{y-1}{2}\)
since y ∈ R = 2
⇒ \(\frac{y-1}{2}\) ∈ R
⇒ x ∈ R
Thus ∀ y ∈ R x ∈ R s.t
f(x) = \(f\left(\frac{y-1}{2}\right)=2\left(\frac{y-1}{2}\right)\) + 1
Thus f is onto.
Hence f is 1 – 1 and onto.
Thus f is bijective.

(ii) Given f : R → R defined by
f(x) = 3 – 4x ∀ x ∈ R
∀ x, y ∈ R such that f(x) = f(y)
⇒ 3 – 4x = 3 – 4y
⇒ x = y
f is one – one.
Let y ∈ R (codomain) be any arbitrary element.
Then f(x) = y
⇒ 3 – 4x = y
⇒ x = \(\frac{3-y}{4}\)
Since y ∈ R
⇒ \(\) ∈ R
∀ y ∈ R ∃ x ∈ R such that
f(x) = \(f\left(\frac{3-y}{4}\right)=3-4\left(\frac{3-y}{4}\right)\) = y
Thus f is onto.
Hence f is one-one and onto
∴ f is bijective.

(iii) Given f : R → R defined by f(x) = 1 + x²
since f (1) = 1 + 1² = 1 + 1 = 2
and f (- 1) 1 +(- 1)² = 1 + 1 = 2
∴ different elements 1 and – 1 have same image in R (codomain)
∴ f is not one-one.
Aliter: ∀ x, y ∈ R such that f(x) = f(y)
⇒ 1 + x² = 1 + y²
⇒ x² = y²
⇒ x = ± y
∴ x ≠ y
Thus f is not one-one.
Let y ∈ R (codomain) be any arbitrary element.
Then f(x) = y
x² + 1 = y
⇒ x = ± \(\sqrt{y-1}\)
for y < 1, x = ± \(\sqrt{y-1}\) ∉ R
∴ f is not onto.
Hence f is neither one-one nor onto.

Question 7.
Let f : R → R be defined as f(x) = x⁴. Show that f is neither one-one nor onto. (NCERT)
Solution:
Given f : R → R defined by f(x) = x⁴
Clearly 1 and – 1 ∈ R but f (1) = f (- 1) = 1
i.e. different elements in R (domain of f) have same images in R (codomain).
Thus f is not one-one i.e. f is many one.
Since – 1 ∈ R. Then f(x) = – 1
x⁴ = – 1
⇒ x = (- 1)^1/4 ∉ R
i.e. – 1 has no pre-images in R (domain)
∴ f is not onto.
Thus, f is neither one-one nor onto.

Question 8.
Show that the function f∴R → R defined by f(x) = cos x is neither one – one nor onto. (NCERT Exemplar).
Solution:
One-one – Since 0, 2 π ∈ R
f(0) = cos 0 = 1 ;
f(2π) = cos 2π = 1
So different elements in R(D_f) have same images in R (codomain).
∴ f is not 1 – 1.
Also, 2 ∈ R (codomain of f).
Then f(x) = 2
cos x = 2 which does not gives any solution
since – 1 ≤ cos ≤ 1
∴ f is not onto.
Hence f is neither one-one nor onto.

Question 9.
Show that the function f∴R → R defined by f (x) = sin² x + cos² x is neither one-one nor onto.
Solution:
Given function f∴R → R defined by
f(x) = sin² x + cos² x ∀ x ∈ R
since f(0) = sin² 0 + cos² 0 = 1
f(π) = sin² π + cos² π
= 0² + (- 1 )² = 1
Thus different elements of R (in domain of f) have same image in R (codomain)
∴ f is many one function i.e. not a one-one function.
Since f(x) = sin² x + cos² x = 1 ∀ x ∈ R
i.e. f (x) be a constant function and all elements in R (D_f) have same image in R.
Since 2 ∈ R (codomain) there does not exists any arbitrary element x ∈ R (domain)
s.t. f(x) = 2
∴ f is not onto.
Hence f is neither one-one nor onto.

Question 10.
Show that the function f : I → 1 defined by f(x) = x² + x is neither one-one nor onto.
Solution:
Given f : Z → Z defined by f (x) = x² + x
Clearly 0, – 1 ∈ Z (domain), here f (0) = 0
f(- 1) = (- 1)² – 1 = 1 – 1 = 0
different elements have same image in Z (codomain).
Thus f is not injective.
also – 1 ∈ Z (codomain) have no. pre-image in Z (domain).
[Let if possible – 1 ∈ Z has pre image x in Z (domain), then f (x) = – 1
⇒ x² + x + 1 = 0
⇒ x = \(\frac{-1 \pm \sqrt{-3}}{2}\) ∉ Z
∴ – 1 has no pre-image in Z]
Thus f is not onto.

Question 11.
If the function f : I → I is defined by f(x) = \(\begin{cases}2 x+1, & \text { if } x \text { is odd } \\ 2 x-1, & \text { if } x \text { is even }\end{cases}\), find
(i) f(3)
(ii) f (4)
(iii) x, if f (x) = – 9.
Solution:
f : I → I defined by (x) = \(\begin{cases}2 x+1, & \text { if } x \text { is odd } \\ 2 x-1, & \text { if } x \text { is even }\end{cases}\)

(i) f(3) = 2 × 3 + 1 = 6 + 1 = 7
[∵ 3 be an odd number ∴ f (x) = 2x + 1]

(ii) f(4) = 2 × 4 – 1 =8 – 1 = 7
[∵ 4 be an even number ∵ f (x) = 2x – 1]

(iii) Given f (x) = – 9
When x is odd then f(x) = 2x + 1
⇒ 2x + 1 = – 9
⇒ x = – 5
When x is even then f (x) = 2x – 1
⇒ 2x – 1 = – 9
⇒ x = – 4
Clearly 3, 4 ∈ I and have same image 7.
∴ different elements of I have same image in I.
∴ f is not one-one.

Question 12.
(i) Show that the function f : N → N is defined by f(n) = \(\begin{cases}n+1, & \text { if } n \text { is odd } \\ n-1, & \text { if } n \text { is even }\end{cases}\) is both one-one and onto.
Solution:
Given f : N → N defined by
f(n) = \(\begin{cases}n+1, & \text { if } n \text { is odd } \\ n-1, & \text { if } n \text { is even }\end{cases}\)

Injectivity:
∀ n, m ∈ N such that f(n) = f(m)

Case I:
If n and m are odd.
Then f (n) = f (m)
⇒ n + 1 = m + 1
⇒ n = m

Case II:
if n and m are even.
Then f(n) = f(m)
⇒ n – 1 = m – 1
⇒ n = m
Thus in both cases, f(n) = f(m)
⇒ n = m.

Case III:
If n is odd and m is even.
f(n) = n + 1 = even ;
f(m) = m – 1 = odd
i.e. n ≠ m
⇒ f(n) ≠ f (m)

Case IV:
If n is even and m is odd
∴ f (n) = n – 1 = odd ;
f (m) = m + 1 = even
i.e. n ≠ m
⇒ f (n) ≠ f (m).
Thus in all four cases; f is injective.

Surjectivity:
if n be any odd number in codomain N ∃ an even natural number n + 1 ∈ N
such that f (n + 1) = n + 1 – 1 = n
If n be any even natural number in codomain N ∃ an odd natural number n – 1
such that f (n- 1) = n – 1 + 1 = n.
Thus f is also surjective.
Hence f is injective and surjective from N to N.
Thus f is bijective.

(ii) Show that the function f : N → N is defined by f(n) = n – (- 1)ⁿ ∀ n ∈ N is bijective.
Solution:
Given f : N → N is defined by
f(n) = n – (- 1)ⁿ ∀ n ∈ N …………..(i)
one – one :
∀ m, n ∈ N, f (n) = f (m)
⇒ n – (- 1)ⁿ = m – (- 1)^m
When n, m both are even or odd
n = m [∵ (- 1)ⁿ = (- 1 )^m = 1 or – 1]

onto:
Let n be an odd natural number e columns in (N)
∴ f (n) = n – 1 [Using (i)]
Thus f (n + 1) = n + 1 – 1 = n
∴ f is onto when n is added
When n is an even natural number ∈ N
Then n – 1 is an odd natural number.
[∵ f (n) = n + 1 Using (i)]
Thus f (n + 1) = n + 1 – 1 = n
So in both cases, f is onto. Therefore f is one-one and onto and hence f is bijective.

Question 13.
Find the number of all one-one functions from the set {1, 2, 3, 4} to itself.
Solution:
A one-one function from {1, 2, 3, 4} to itself be a permutation on four symbols 1, 2, 3, 4.
Thus, the total number of one-one functions from {1, 2, 3, 4} to itself is same as the total number of permutations on four symbols 1, 2, 3, 4, which is equal to 41.
Hence the total no. of 1 – 1 functions from {1, 2, 3, 4} to itself = 4! =24.

Question 14.
Show that the function f : Q → Q defined by f (x) = 3x – 2 is one-one.
Solution:
Given f : Q → Q be defined by
f{x) = 3x – 2 ∀ x, y ∈ Q s.t
f (x) = f(y)
⇒ 3x – 2 = 3y – 2
⇒ 3x = 3 y
⇒ x = y
∴ f is one-one.

Question 15.
Show that the function f : N → N defined by f (x) = 2x – 1 is not onto.
Solution:
Given function be f : N → N defined by f(x) = 2x – 1
Clearly 2 ∈ N.
Then f (x) = 2
⇒ 2x – 1 = 2
⇒ x = \(\frac{3}{2}\) ∉ N
Thus element 2 has no pre-image in N (domain of f)
∴ f is not onto.

Question 16.
Show that the function f : N → N defined by f (n) = n² is injective.
Solution:
Given function of f : N → N defined by
f(n) = n²
∀ n, m ∈ N s.t f (n) = f (m)
⇒ n² = m²
⇒ (n – m) (n + m) = 0
⇒ n = m [∵ n + m > 0 ∀ n, m ∈ N]
∴ f is one-one i.e. injective.

Question 17.
Is the function f : N → N defined by f (m) = m² + m + 2 one – one ? Justify your answer.
Solution:
Given f : N → N defined by
f (m) = m² + m + 2
∀ n, m ∀ N s.t f (n) = f (m)
⇒ n² + m + 2 = m² + m + 2
⇒ n² – m² + n – m = 0
⇒ (n – m) (n + m + 1) = 0
⇒ n – m = 0 [∵ n + m + 1 > 0 ∀ n, m ∈ N]
⇒ n = m
Hence f is injective i.e. one-one.

Question 18.
What is the range of the function f(x) = \(\frac{|x-1|}{x-1}\) ?
Solution:
Let y = f (x) = \(\frac{|x-1|}{x-1}\), x ≠ 1
For x – 1 > 0
⇒ | x – 1 | = x – 1
∴ f (x) = \(\frac{|x-1|}{x-1}\) = 1 [∵ x ≠ 1]
For x – 1 > 0
⇒ |x – 1| = x – 1
∴ f (x) = \(\frac{x-1}{x-1}\) = 1 [∵ x ≠ 1]
For x – 1 < 0
⇒ |x – 1| = – (x – 1)
∴ f(x) = – \(\frac{(x-1)}{x-1}\) = – 1
Thus, R_f = {- 1, 1}.

Question 19.
Find the domain of the function f(x) = \(\frac{1}{5-3 \sin x}\).
Solution:
Given f(x) = \(\frac{1}{5-3 \sin x}\)
For D_f : f (x) must be a real number 1
⇒ \(\frac{1}{5-3 \sin x}\) must be a real number.
⇒ 5 – 3 sin x ≠ 0, which is true ∀ x ∈ R
[∵ – 1 ≤ sin x ≤ 1
⇒ 3 ≥ – 3 sin x ≥ – 3
⇒ 5 + 3 ≥ 5 – 3 sin x ≥ 5 – 3
⇒ 2 ≤ 5 – 3 sin x ≤ 8]
Hence D_f = R

Question 20.
Find the range of the function f (x) = \(\frac{1}{2-\cos x}\) (NCERT Exemplar)
Solution:
Let y = f (x)
= \(\frac{1}{2-\cos x}\)
since – 1 ≤ cos x ≤ 1
⇒ 1 ≥ – cos x ≥ – 1
⇒ 2 + 1 ≥ 2 – cos x ≥ 2 – 1
⇒ 1 ≤ 2 – cos x ≤ 3
⇒ 1 ≥ \(\frac{1}{2-\cos x}\) ≥ \(\frac{1}{3}\)
⇒ \(\frac{1}{3}\) ≤ y ≤ 1
∴ R_f = [\(\frac{1}{3}\), 1]

Question 21.
Find the range of the following functions:
(i) f (x) = sin x + cos x
(ii) f (x) = 3 sin x + 4 cos x.
Solution:
(i) Given f (x) = sin x + cos x
putting 1 = r cos ∝ ; 1 = r sin ∝
On squaring and adding ; we have
r² = 2
⇒ r = √2
On dividing ;
tan ∝ = 1
⇒ ∝ = \(\frac{\pi}{4}\)
f(x) = r cos ∝ sin x + r sin ∝ cos X = r sin (x + ∝)
⇒ F (x) = √2 sin (x + \(\frac{\pi}{4}\))
Since – 1 ≤ sin (x + \(\frac{\pi}{4}\)) ≤ 1
– √2 ≤ √2 sin (x + \(\frac{\pi}{4}\)) ≤ √2
⇒ – √2 ≤ y ≤ √2
∴ R_f = [- √2, √2]

(ii) Given f(x) = 3 sin x + 4 cos x ……………(*)
putting 3 = r cos ∝
4 = r sin ∝
On squaring and adding (L) and (2) ; we have
r² = 3² + 4²
r = \(\sqrt{25}\) = 5
On dividing (2) by (1) ; we have
tan ∝ = \(\frac{4}{3}\)
⇒ ∝ = tan^-1 (\(\frac{4}{3}\))
from (*) ; f (x) = r cos ∝ sin x + r sin ∝ cos x
⇒ f (x) = r sin (x + ∝)
= 5 sin (x + ∝)
since – 1 ≤ sin (x + ∝) ≤ 1
⇒ – 5 ≤ 5 sin (x + v) ≤ 5
⇒ – 5 ≤ f (x) ≤ 5
∴ R_f = [- 5, 5]

Question 22.
The function f : R → R is defined by f (x) = |2x – 3|.
(i) Is f one-one ?
(ii) Is f onto ?
Solution:
(i) Given f : R → R defined by
f(x) = | 2x – 3 | ∀ x ∈ R s.t f(x) =f (y)
⇒ | 2x – 3 | = | 2y – 3 |
⇒ 2x – 3 = ± (2y – 3)
⇒ 2x – 3 = 2y – 3 or 2x – 3 = – 2y + 3
⇒ x = y or x + y – 3 = 0
Thus f is not one-one.
Further, 4, – 1 ∈ R, f (4) = | 8 – 3 | = 5 ;
f (- 1) = |- 2 – 3| = |- 5| = 5
i.e. different elements of R have same images in R.
Thus f is not one-one.

(iii) since – 1 ∈ R thenf (x) = – 1
⇒ | 2x – 3 | = – 1, which is impossible
Since | 2x – 3 | > 0 ∀ x ∈ R
Thus, negative real numbers have no pre-images in R.
∴ f is not onto.

Question 23.
If A = {1, 2, 3} and B = {3, 5}, then find the number of functions from A to B.
Solution:
Given A = {1, 2, 3} and B = {3, 5}
Here n (A) = 3 ; n (B) = 2
∴ required no. of functions from A to B = [n (B)]^{n (A)}
= 2³ = 8

Question 24.
If A = {a, b, c} and B = {1, 2, 3, 4}, then find the number of functions from A to B.
Solution:
Given A = {a, b, c} and B = {1, 2, 3, 4}
Here n (A) = 3 ;
n (B) = 4
∴ required number of functions from A to B = [n (B)]^{n (A)} = 4³ = 64.

Question 25.
If A = {a, b} and B = {1, 3, 5}, then find the number of one-one functions from A to B.
Solution:
Given A = {a, b}
∴ n (A) = 2 = m
and B = {1, 2, 5}
∴ n (B) = 3 = n
∴ required no. of one-one functions from A to B
= \({ }^n \mathrm{P}_m\)
= \({ }^3 \mathrm{P}_2\)
= 3! = 6
[∵ no. of one-one functions from A to B
= \(\left\{\begin{array}{ccc}
{ }^n \mathrm{P}_m & ; m \leq n \\
0 & ; m>n
\end{array}\right.\)
where n (A) = m and n (B) = n]

Question 26.
If A = {a, b, c} and B = {p, q}, then find the number of onto functions from A to B.
Solution:
Given A = {a, b, c} and B = {p, q}
Here n (A) = 3 = m ; n (B) = 2 = n
∴ required no. of pnto functions from A to B
= \(=\sum_{r=1}^2(-1)^{2-r}{ }^2 \mathrm{C}_r r^3\)
[∵ no. of onto functions from A to B
= \(\left\{\begin{array}{cc}
\sum_{r=1}^n(-1)^{n-r n} C_r r^m & ; n \leq m \\
0 & ; n>m
\end{array}\right.\)
= (- 1)^{2 – 1 2}C₁ 1³ + (- 1)^{2 -1 2}C₂ 2³
= – 2 + 1 × 8 = 6

Question 27.
If A = {1, 2, 3, 4} and B = {- 1, 3}, then find the number of onto functions from A to B.
Solution:
Given A = {1, 2, 3, 4} and B = {- 1, 3}
∴ n (A) = 4 = m ; n (B) = 2 = n
∴ required no. of onto functions from A to B
= \(\sum_{r=1}^2(-1)^{2-r}{ }^2 \mathrm{C}_r r^4\)
= (- 1)^{2-1 2}C₁ 1⁴ + (- 1)^{2 – 2 2}C² 2⁴
= – 2 + 16 = 14.

Question 28.
If A = {1, 2, 3} and B = {a, b, c}, then find the number of one-one onto functions from A to B.
Solution:
Given A = {1, 2, 3} and B = {a, b, c}
∴ n = n (A) = 3 ;
m = n (B) = 3
Here n = m = 3
∴ required no. of one-one onto i.e. bijection from A to B = 3! = 6
[∵ Total no. of bijections from A to B = \(\left\{\begin{array}{cc}
n ! ; & n=m \\
0 ; & n \neq m
\end{array}\right.\)
where n (A) = m ; n (B) = n]

Question 29.
If A = {1, 2, 3, 4} and B = {a, b, c}, then find the number of bijections from A to B.
Solution:
Given A = {1, 2, 3, 4} ; B = {a, b, c}
∴ n (A) = m = 4 ;
n (B) = n = 3
Here m ≠ n
Thus, the required no. of bijections from A to B = 0
[∵ Total number of bijections from A to B = \(\left\{\begin{array}{cc}
n ! ; & n=m \\
0 ; & n \neq m
\end{array}\right.\)
where n(A) = m; n(B) = n].

Question 30.
Which of the following graphs represent functions ?

Solution:
(i) From graph, we observe that, every element has a unique image i.e. corresponding to one value of x, we have (unique) one value of y and given graph is a continuous curve without any break.
∴ given graph represents a function.

(ii) From graph, it is observe that corresponding to one value of x we have two values of y,
i.e. one above and one below the x-axis. Thus for one value of x, we does not have unique value of y.
∴ given graph does not represents a function.

(iii) From graph, it is observe that its most likely eqn. be y² = 4ax where a > 0
Clearly for one positive value ofx, we have two values of y. Thus given graph does not represents a function.

(iv) From graph, it is observe that, its approximate eqn. be x² = – 4 ay where a > 0 So for one negative value of y we have two values of x. Also corresponding to one value of x we have unique value of y.
Further given curve is continuous without any breaks.
∴ given graph represents a function.

Question 31.
From the graphs of the following functions in x, find their range :

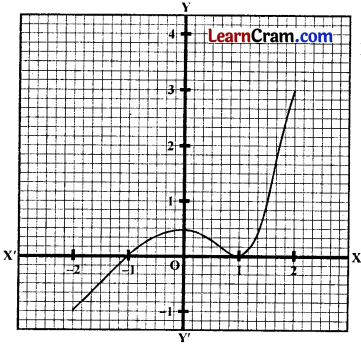
Solution:
(ï) From graph, it is observe that, the values of y varies from — 1 to 3.
∴ R_f = [- 1, 3]
(ii) From graph, it is observe that values of y varies from — 1 to 3 except 2.
∴ R_f = [- 1, 2) ∪ (2, 3]
= [- 1, 3] – {2}

Question 32.
Which of the following graphs represent a one-one function ?

Solution:
(i) From graph, it is observe that, the curve cuts x-axis at three points. Thus three different values of x, we have same value of y i.e. y = 0. Thus different elements in domain of f have same images i.e. ∴coordinate of point in (co domain of f)
∴ f is not 1 – 1 and it is many one.

(ii) Since the graph never cuts the x-axis other than (0, 0). Hence different values of x (in domain off) have different values of y (in co domain of f). Thus f is one-one.